1. Частотно-контурные понятия объёмов и сила падения.

Ещё Н. Коперник в его первом требовании призывал воспринять то обстоятельство, что «не существует одного центра для всех небесных орбит или сфер» (см.12, стр.420), чем он фактически отрицал гелиоцентризм, как придание планетному вращению одного центра в виде Солнца. Потому реально существующая планетная система – это не гелиоцентризм и не планетарное вращение (также обозначающее один центр для всех орбит), а взаимно-центрическая планетная система и взаимно-центрическое именно планетное вращение. Вот потому и третий закон И. Кеплера, гласящий, что «квадраты сидерических периодов обращения двух планет относятся как кубы больших полуосей их орбит», отражает как раз взаимно-центрическую полевую структуру в виде равенства соотношения сферических (Т2) и окружных ((4/3)*πиR3) объёмов пространства, образованных обращением двух планет (см. 2, стр. 300). Ведь это равенство переводится во взаимно-центрическое сопряжение сферического и окружного объёмов планетных пространств, а затем - в соотношение сферического и окружного объёмов области пространства, образованной обращением каждой планеты: Т2/ (4/3) πR3 .

Сферический пространственный объём в виде квадрата периода вращения означает сопряжение периодов вращения контурной (k) и частотной (q) полевых образующих вращения или окружных полевых плоскостей(2πи)k и (2πи)q, перпендикулярных друг к другу в их вращательном сопряжении. В одном из изложений стандартной модели элементарных частиц – это круговые полевые слои, что подчёркивает общее применение физики различения (без разделения на механику и квантовую физику). Сферический объём, как образующий в его движении самого себя, можно назвать квадратом периода частотно-контурного или полевого заполнения объёма пространства. Потому он представим голографическим изображением объекта. В термодинамике понятие сферического объёма отражается в понятии объёма пространства импульсов, поскольку в физике различения импульс – это величина, обратная периоду, т.е. частота (см. 1, стр. 81). Размерность сферического объёма, как квадрат длительности, подтверждается и различение уравнения Карно-Клайперона (V*P/T=const), постоянность которого, выражаемая структурной единицей размерностей величин (см.2, стр. 346), может быть только при частотно-контурных размерностях не только объёма «V» (как сферического объёма), но температуры «T» (в виде частоты сферическо-окружного объёмного преобразования) и давления «V» (в виде третьей степени частоты «1/сек3» молекулярного поля).

Частотно-контурное обозначение давления для газов – это отношение их внутримолекулярной частоты к занимаемому ими сферическому объёму. В открытом же пространстве космического вакуума и в отношении к полевым образованиям – это уже не давление, а интенсивность поля, необоснованно называемая в старой физике напряжённостью. И это отношение структурной полевой частоты (например, гравитационной частоты лунно-земного вращения) к единице сферического объёма. Ведь гравитация - это не натянутая сетка на батуте, а подвижная полевая структура вокруг нас, образующая в этой подвижности и самое себя, и окружающий мир.

При этом сферический и окружной объёмы пространства означают и сам сферическо-окружной пространственный переход в виде постоянной инверсии трёх видов полевых объёмов (см.5, стр. 179). Исходный сферический объём (в виде спирального вращения вокруг друг друга увеличивающихся и уменьшающихся полевых сфер) выделяется из пространства именно перпендикулярным сопряжением периодов вращения, ограничиваясь снаружи, и будучи этим объёмом без фиксированного центра, а значит, и без определённого радиуса. Сопряжение образующих вращения ((2πи)k*(2πи)q) в этом случае происходит через перпендикулярный разворот, как раз и образующий сферу, чем оно получает вид«(2пи) k *(2πи)q/(πи/2)=8πи». Такой разворот обозначает переходное полевое пространства (о чём см дальше) и межпланетное полевое пространство (пространство полевых планетных сфер). Кстати, в поле силы тяжести такое сопряжение идёт без перпендикулярного разворота, чем образуется вид«4πи2». В этом виде объёма его центр вещественно или размерно не проявлен. В предмассовом полевом пространстве сопряжение полевых образующих вращения идёт через полу-окружной разворот на две стороны, обозначая этим уже радиус сферы: ((2пи)k *(2πи)q/πи)*R=4πиR.

Это уже переходный сферический объём в виде квадруполя или квадрупольный объём с обозначением центра лишь по плоскости вращения (чем, кстати, эта плоскость и образуется в движении планет). Такой вид сферического объёма подтверждается и тем, что, исходя из формулы оборотного маятника при обозначении «ускорения» свободного падения или заряда поля силы тяжести величиной g0, равной 3,124 (без числа «пи»), формула сферического объёма получает вид:Vs=T2 = 4πR/g0 . Окружной же объём отражается в термодинамике понятием объёма пространства координат, означая преобразование подвижно-полевого сферического объёма (как полевой сферы) в объём воспринимаемо стационарный (в виде геометрической объёмной фигуры), т.е. - в объём уже массового полевого пространства. В окружном объёме его центр уже выделяется из полевого пространства, будучи центром по всем трём взаимно-перпендикулярным плоскостям. Этот объём представим изометрическим изображением геометрической фигуры и её симметричным сечением. Для сферы окружной объём записывается в виде выражения «(4/3) * пиR3», что можно обозначить тройным сопряжением полевого квадруполя с его радиусом из-за расслоения квадрупольного объёма по трём взаимно-перпендикулярным полевым осям (останавливающим этим полевое вращение и проявляющим воспринимаемое нами вещество).



При этом в подвижно-полевом обозначении радиуса, как величины приведённой к единице, окружной объём сферы VR = (4/3) пиR3 около 4 % или в 1,041 раза (3,124/3) больше объёма сферического. Соотношение сферического (подвижно-полевого) и окружного (статичного) объёмов одной и той же области пространства, естественно, даёт постоянное значение. Вот потому равенство соотношений Кеплера переводится вначале в равенство взаимно-центрических сопряжений сферического и окружного объёмов пространства двух планет, а затем – в отношение сферического и окружного объёмов областей пространств, образованных обращением планет, а не в некую постоянную числовую величину, как воспринимается. Соотношение «Т2/ (4/3) пиR3» есть и геометрическим (точнее, пространственно-метрическим) выражением сферическо-окружного или пространственно-полевого перехода магнитной структурной частоты 106 «(πи/2: πи/√2: πи / πи: πи/√2: πи/2)», что исходит из различения постоянной тонких полевых структур Зоммерфельда и скорости перехода причины в следствие Н. Козырева (см. 2, стр.24). Это значит, что магнитная структурная частота – это начальная частота пространственно-полевого преобразования. Вот потому эффект Эйнштейна – де Хааза, где ферро-магнитный образец после его намагничивания получает момент вращения относительно направления намагничивания, проявляется и в образовании планетного вращения Земли в виде симметричного (относительно земной оси) смещения магнитных полюсов (см.1, стр. 342). Отсюда вращение вокруг оси планеты может быть только при наличии у неё магнитного поля, а магнитный момент магнитного поля планеты образует и её момент вращения. Т.е. сначала проявляется исходное пространственное магнитное поле, выражаемое структурой частотной или полевой воды (см. 5, стр. 34) как расслоенного или плоскостного состояния этого поля, а потом - его инверсия с образованием вращения планеты и с проявлением уже воспринимаемого нами магнитного поля, а затем – поля электрического.

Приведённое полевое объёмное преобразование можно выразить и в различении пути падения тела, переходящего или инвертирующего в его орбитальное вращение, и даже - при определении веса тела. Это значит, что полевой подход квантовой физики, например, в стандартной модели элементарных частиц, распространяется, оказывается, и на физику механики, как на квантовую механику. Старая же физика оперирует квантовыми понятиями только для «планковских» (чрезвычайно малых) величин, а потому реальная квантовая механика теории различения - это уже универсально-квантовая или полевая механика.

Прежде всего надо уяснить, что, если есть движение падения, то есть и сила падения, образующая это движение (см. 2, стр. 286). Сила падения (одинаковая для всех тел или независимая от массы тела) - это сила, увлекающая тело в падение и образующая силу тяжести, как уже зависимую от массы тела, т.е. проявляющая массу тела. Сила согласно физике различения, различается на контурную силу, прикладываемую к конкретному телу и на частотную силу в виде общего полевого движения, увлекающего тела, т.е. как подобие гравитационного объёмно-вихревого (полевого) потока. Сила падения – это как раз частотная сила в размерности импульса силы по физике различения (1/сек2).

При этом частотная сила падения «Fп.» выражается контурной величиной заряда поля силы тяжести («ускорения» свободного падения «g» в старой физике), т.е. без числа «пи»: Fп.=g0=g/пи = 3,12 «1/сек2» (см.1, стр. 125). Величина «пи», как обозначение движения полевого перехода, имеет размерность «м». Размерность импульса силы по физике различения получает и сила планетного вращения, и сила орбитального вращения (инвертирующие в силу падения). Контурная или наружная сила в физике различения образуется произведением внутренней силы (как преобразования внутренней энергии в виде частоты) на импульс силы, получая размерность «кг/сек2» (см.1, стр.82; 2, стр. 286). Сила тяжести «Fт.» – это как раз контурная сила. В виде внутренней силы здесь выступает начальная масса тела «m0», численно равная отношению веса тела «Р» к частотной или полной величине «g», как полевой единицы взаимодействия, т.е. как в данном случае безразмерной величины.

2. Вес, образуемый работой силы тяжести.

Т.о, сила тяжести – это произведение начальной массы тела «m0» в размерности «кг» на контурную величину «g0» в размерности импульса силы (Fт.=m0*g0). получая размерность «кг/сек2». Полная же масса тела «m» – это отношение веса тела «Р» к контурной величине «g0» заряда поля силы тяжести уже в размерности заряда вращения или «м/сек2», получая размерность «кг*сек2/м». Эта размерность выражается и как отношение общей или суммарной внутримолекулярной стягивающей полевой силы к общему молекулярному заряду тела (см. 5, стр. 127). Т.е. начальная масса меньше полной или проявленной массы на величину «пи». Отсюда и вес тела, как полностью проявленная масса, больше силы тяжести на величину «пи». Вот потому, например, при взвешивании на весах не сразу образуется окончательное их показание. Величина «пи», обозначающая полевой переворот или переход в виде вертикального полу-вращения, означает преобразование силы тяжести, как переходного полевого образования в окончательный полевой объём массового пространства. При этом необходимо отметить и ещё один момент.

Размерность силы тяжести и вообще силы, применяемой в старой физике в виде одного «ньютона» или «кг*м/сек2» - это в реальности по физике различения уже работа силы. Потому, кроме силы тяжести, проявляемой телом, меньшей значения веса тела на величину «пи», необходимо различать работу силы тяжести «Ат.», проявляющей вес тела. Это как раз произведение силы тяжести на величину «пи» (Ат=Fт.*пи), как стягивание полевой окружности (перпендикулярной к наблюдателю или невидимой ему) в точке контакта тела с опорой в точку, чем она получает размерность единицы длины «м.». Работа силы тяжести, проявляющая полную массу тела, численно равна весу тела. Но вес тела выражается в общепринятой размерности «кг», а потому, как физическая величина, - это произведение полной массы тела на контурную величину «g0» (Р=m*g0) в размерности заряда вращения или «м/сек2». В старой же физике отсутствует понятие силы падения, а категории силы тяжести, веса и массы не имеют конкретного физического определения, поскольку фактически равны друг другу, поскольку придаётся эталон массе в виде значения веса платиноиридиевой гири (в размерности «кг»).

Более того, употребляемая в старой физике размерность массы «кг» означает, что и плотность вещества привязана к весу тела, что исключает её, как физическую категорию в невесомости космоса. И напомним, что якобы равное ускорение падающих тел - это следствие иллюзии наблюдения пути падения, близкого к прямой линии, но образуемого в реальности полевым инверсионным вращением. Этим и объясняется, что падающее тело стремится вращаться. При этом разная скорость падения при разных значениях пути падения - это не ускорение, а полевая структура движения падения, разбираемая ниже, как проявление пространственно-полевого (сферическо-окружного) перехода. Ускорения, в том числе и равного при падении быть не может, хотя бы потому, что утверждение противоречит явлению невесомости при падении. Ведь любое ускорение проявляет массу. И если бы было некое равное ускорение, то проявлялась бы и некая равная масса, а значит, и вес. А вот линейное ускорение (ускорение как таковое) это постоянное на данном отрезке времени изменение скорости, приводящее к проявлению массы и веса тела.
Напомним, что поле силы тяжести космических тел можно разделить на поворотные поля силы тяжести (силы падения), как явно проявленные поля планет и отдельных спутников (например, Титана), и - на спиральные слабые поля спутников планет, астероидов и комет. Поворотные поля силы тяжести образуются наружно-молекулярной полевой оболочкой планет и их вращением вокруг внутреннего окружного центра (считаемого неким «барицентром»), образующим их суточное вращение. Отчего эти поля и получают инверсионную или поворотную структуру вместе с образованием их вращения вокруг оси.

Спиральные же слабые поля образуются у космических тел только за счёт их наружно-молекулярной полевой оболочки, вращающейся вместе с телом, как не имеющим собственного окружного центра, из-за чего эти тела не получают и одно-центрового вращения вокруг оси, как оси тела (подобно юле). Вот потому, например, спутники, космические аппараты и астероиды вращаются, двигаясь только по окружности, т.е. не имеют собственного вращения вокруг оси, как такового. В связи с этим и интенсивность поля силы тяжести Луны (в виде «ускорения» свободного падения) составляет величину, намного меньшую принятой в теории гелиоцентризма. И, исходя из месячного лунно-земного вращения и меньшего примерно в 3,6 раза диаметра Луны её весовая гравитация составляет лишь около 9 % от интенсивности поля силы тяжести Земли ((9,8/30)/3,6) Т.е. тело, имеющее вес на Земле в 100 кг., на Луне будет весить всего около 9 кг., падая по явно спиральной или параболической траектории (сразу в сторону). И можно сказать, что поворотное или явное поле силы тяжести, как поле одно-центровое, проявляет именно окружной объём пространства. Подобно и магнитное поле уже в массовой полевой фазе пространства, как также одно-центровое, явно проявляется лишь у планет, имеющих вращение вокруг их внешнего окружного центра (образующего их годовой оборот).

В связи с этим и заряд поля силы тяжести («ускорение» свободного падения) «g», переходящий в заряд поля планетного вращения, можно рассматривать относительно трёх видов полевых объёмов. В старой физике совершенно необоснованно и искусственным образом уравнивают силу тяжести (что есть в реальности уже работой силы тяжести) «F=m*g» с формулой «G*(m*Mз)/R2», исходящей из неверного понимания гравитации взаимодействием двух масс, где m и Mз – масса соответственно тела и Земли, но не различаемые фактически от категории веса (см. 5, стр.126).

В реальности же величина «g» находится не из такого надуманного равенства, а - из формулы высоты падения «h» Галилея «g=2h/T2» и из формулы оборотного маятника «g=4пи2h/T2» (см. 16, стр. 906), где «h» - расстояние между параллельными осями подвеса маятника. Кроме того, исходя из понимания величины «g» в старой физике центростремительным «ускорением» при определении космической скорости (см. 17, стр.73), величина «g» выражается, как «4пи2R/T2» (см. 17, стр.31), где «R» –радиус вращения. Отсюда при равенстве во всех формулах периода «T» одной и той же величине, как приведённой единице, возникает тождественное выражение "2h≡4πи2h≡4πи2R" , которое однозначно указывает на инверсионную полевую структуру пространства. Т.е., расстояние между подвесами маятника «h» тождественно радиусу вращения «r», а высота падения «h» тождественна выражению «2пи2R», где «пи» в квадрате означает сопряжение радианных поворотов «пи», как двух взаимно-центрических полевых поворотов в двух перпендикулярных плоскостях.



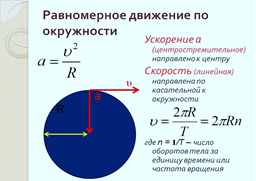
Так вот относительно окружного объёма нашей массовой фазы пространства величина «g» выражается, как «4пи2R/T2» или в виде «V2/R», поскольку в старой физике центростремительное «ускорение» равно отношению квадрата скорости, как скорости вращения (2пиR/Т), к радиусу (см. 17, стр.30), что изображено на рисунке выше. Относительно переходного полевого объёма величина «g» принимает контурный вид g0 без числа «пи» «4пиR/Т». Но всемирная гравитационная полевая структура пространства говорит об обратной зависимости от квадрата радиуса. Потому относительно сферического полевого объёма величина «g» выражается в виде «4пи2/T2», т.е. – в размерности частотной силы падения и силы вращения (1/сек2). Этим для размерной величины, равной единице (например, одному метру), заряд поля силы тяжести (силы падения) относительно плоского (вне-объёмного) восприятия в нашей фазе пространства становится частотой 3,13 «1/сек», как корень квадратный из величины «g». Т.е. «ускорение» свободного падения – это в полевой реальности пространственно-полевая частота.

А это значит, что величина «g» воспринимается «ускорением» свободного падения, а падение – неким равноускоренным движением только при определении скорости и высоты падения, когда падающее тело вступает в контакт с поверхностью, или, например, фиксируется его положение лазером. Этим обозначается и наша массовая фаза пространства. Иначе говоря, из-за пространственно-полевого перпендикулярного поворота «пи/2» (образующейся и в структуре падения, о чём речь дальше) общая для всех тел частота «1/ T=√g», одинаково увлекающая их в падение, при обозначении нашей полевой фазы пространства инвертирует уже в скорость вращения 2пиR*(1/Т), зависящую от полевого радиуса, а значит, - и от высоты падения. При этом и скорость вращения воспринимается уже линейной скоростью (по линии падения). Приведённое явление сравнимо с принципом неопределённости в квантовой физике, когда при определении одного параметра (например, координаты частицы) другой параметр (например, импульс), как определимый уже только в плоскости, перпендикулярной к первой, воспринимается относительно неё неопределимым. Это явление в физике различения названо вращательным параллаксом, как различной окружной скоростью на фоне единой частоты вращения, наблюдающейся в полевой плоскости, уже перпендикулярной к первой.

3. Нереальность понятия ускорения силы и инверсионная структура поля силы падения (силы тяжести).

Таким образом, то, что равномерное вращение каждой точки плоскости окружности согласно старой физике происходит якобы «с ускорением, направленным в каждой точке окружности её центру» (см. 17, стр. 29) – это следствие иллюзии вращательного параллакса, как свойства дискретности нашей полевой массовой фазы пространства. Здесь, как и в принципе неопределённости, когда второй параметр становится неопределимым при установлении первого, движение, определённое равномерным в виде общей частоты вращения, после определения радиуса вращения, т.е. при выделении конкретной точки в общем вращении, вдруг получает разную скорость. При этом изменение периода вращения точки на окружной плоскости относительно другой точки приводит к иллюзии её отставания или опережения, как к иллюзии её отдельного вращения, что и происходит при наблюдении планет относительно солнечно-земного вращения. Изменение же самого радиуса точки относительно единого периода вращения окружной плоскости (как единой частоты) приводит в таком полевом повороте «пи/2» к иллюзии изменения её скорости, но что необоснованно называется неким «равноускоренным» движением.

Скорость при падении действительно зависит от высоты падения, причём – инверсионно или по параболическому закону (что показано ниже), причём – только при определении этой высоты (например, в результате контакта с опорой). Но это никак не изменение категории ускорения в старой физике, поскольку выражение величины «ускорения» (в реальности заряда вращения) и в виде «V2/R» и в виде «4пи2R/T2» исключает возможность её изменения при изменении радиуса. Ведь одна и та же величина не может одновременно и расти, и уменьшаться, называясь то центростремительным, то центробежным «ускорением». Об этом свидетельствует и величина «g», которая вовсе не изменяется пропорционально высоте падения, а зависит лишь от расстояния до центра Земли, причём - от квадрата этого расстояния (как выражения полевой взаимо-центричности). В этой связи абсурдны и сами понятия центростремительного и центробежного ускорения, а так называемые центробежные и центростремительные силы – это в реальности обозначения контурных и частотных полевых окружностей, образующих сферу вращения и переходящих или инвертирующих друг в друга (см.5, стр. 215). Отсюда абсурдно в старой физике и вообще само понятие ускорения, как скорости изменения скорости, поскольку по размерности физики различения (квантовой механики) эта величина обозначает уже работу силы и заряд силовой полевой сферы, аналогичный заряду поля силы тяжести (силы падения).

Абсурдно потому и определять силу произведением массы на такое ускорение. Т.е. применяемая в старой физике категория ускорения отсутствует в природе. Ускорение, как и замедление – это изменение скорости за определённое время, которое неизменно для характеристик данного процесса, приводящее к инерционным (также полевым) явлениям, например, в виде перегрузок, но никак не скорость изменения скорости.
В связи с вышеизложенным пространственно-полевой переход (п-п переход) исходной магнитной структурной частоты 106 наиболее явно проявляется в структуре траектории падения тела, поскольку это явление все могут наблюдать в любое время. Падение в нашей окружной полевой фазе пространства с её окружным объёмом мы привыкли воспринимать также одно-центровым движением тел к центру Земли в каждой точке земной поверхности. Но, оказывается, это лишь иллюзия нашего восприятия, стоит лишь рассмотреть хотя бы причину появления числа «два» в знаменателе формулы пути падения. Путь падения «h», исходя из того, что величина «g» выражает в старой физике в понятие «ускорения», как отношение изменения скорости к длительности этого изменения, должна выражаться в виде «h=g*t2».

Но в знаменателе появляется «двойка» именно потому что, величина "g", выражая полевое движение вращения, относится к вращению, т.е. – к полевой окружности «2пиR», образуемой её контурной (силовой) и частотной полуокружностями, перпендикулярными друг к другу. Этим определяемая высота падения – это обозначение второй части полевой окружности, как контурной полуокружности «пR=h». Т.е., траекторию падения мы воспринимаем длиной дуги земной окружности (близкой к прямой линии), но в реальности по формуле «h=g*t2/2» определяем радиус полевой полуокружности с диаметром, равным расстоянию между точкой начала падения и точкой контакта тела с поверхностью. Иначе говоря, в виде пути падения в нашей массовой фазе пространства обозначается радиус полуокружности, а не диаметр из-за образования падения вращением, в связи с чем любое падающее тело и стремится вращаться. На полевом же, реальном уровне (предмассового полевого пространства) появление «двойки» в знаменателе формулы «h=g*t2/2» объясняется возникновением полевой полуокружности вместо полной окружности.
Это значит, что если выразить величину заряда поля силы тяжести «g» произведением контурной величины g0 на число «пи», то путь падения преобразуется уже в радиус, как в половину указанного расстояния (пR=g*t2/2: R=g0*t2/2), чем определяемая высота падения и сокращается вдвое.

Надо обратить внимание на то, что поскольку диаметр в полу-вращении проявляется радиусом, то путь падения образуется полевым взаимно-центрическим вращением полевых сфер вокруг друг друга, общий диаметр качения которых растёт вместе с увеличением пути (см. рисунок ниже слева). И в моментальной фотографии нашей фазы пространства эта структура вращения представляет собой полевой дипольный или восьмеричный вид с общим диаметром, как с ожидаемым путём падения (исходя из формулы «h=g*t2»). Но при контакте тела с опорой (при прекращении падения) такая структура складывается в одну полевую окружность, составленную уже из двух полуокружностей, диаметр которых равен радиусу предыдущего дипольного образования, как половины ожидаемого пути падения (см. рис. ниже справа). Образование полевой окружности падения доказывается и самим фактом колебания маятника.



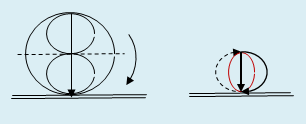
При этом и радиус полевой окружности (как реально определяемый путь падения) с ростом высоты падения проявляется в виде уже длины окружности, перпендикулярно (на радианную величину «пи/2) развёрнутой к этому радиусу и, соответственно, - к наблюдателю, что показано красной окружностью на рис. выше. Ведь при контакте тела с опорой после падения (например, в виде удара) образуется силовая полевая сфера, состоящая из двух перпендикулярных друг к другу уже сферических образующих, как полных окружностей. Этим радиус падения образуется перпендикулярно к нему развёрнутой полевой окружностью, как сферической контурной образующей. Т.е. падение тела образуется перпендикулярными друг к другу полевой полуокружностью (проявляемой радиусом падения) и полной полевой окружностью (образующей радиус падения).

Именно полная полевая окружность и увлекает полевое взаимно-центрическое вращение в движение падения, проявляя этим полевую наружно-молекулярную оболочку Земли. При этом значение радиуса падения, численно равное величине контурной «g0», что есть приведением полевой окружности (в виде сферической образующей) к единице взаимодействия, даёт величину около 19,6 м. (см. 5, стр. 114).
Т.о., можно сказать, что лишь до высоты падения 19,6 м., примерно соответствующей и высоте опытов Галилея, однозначно проявляется действие формулы «h=g*t2/2». Если же величину «g» в формуле «пR= g*t2/2» выразить формулой оборотного маятника (g=4?2R/T2), то появляется инверсионное тождество «R?2?R». Здесь радиус, как расстояние между точками подвесов двух маятников (образующих оборотный маятник), означает как раз путь падения в виде расстояния между точкой начала и окончания падения, но становящегося уже длиной этой полевой окружности. В связи с этим путь падения на высотах, превышающих величину около 19,6 м., в структурной или в инверсионной записи выглядит, как «пиR: (D) R: 2пиR», чем радиус траектории падения можно назвать инверсионным радиусом падения.

Отсюда, чем больше путь падения, тем более отчётливо проявляется приведённая его структурная инверсия в виде полевой полуокружности, образуемой полной полевой окружностью, перпендикулярно развёрнутой к первой, что как раз и создаёт иллюзию некоего «равноускоренного движения».
Т.о., путь падения тела, воспринимаемый нами близким к прямой линии, как к дуге земной окружности, в начальном рассмотрении и в полевой реальности представляет собой полуокружность, а замеряемое расстояние уже в воспринимаемой нами реальности окружного объёма означает диаметр «D», но инвертирующий в радиус «R» при контакте с опорой. Это значит, что полевые контурные и частотные образующие окружности вращения, как полевое дипольное или восьмеричное образование, в нашем окружном объёме пространства за счёт радианного поворота «пи» «свёртываются» вокруг горизонтальной оси в единую полевую окружность, диаметр которой и есть определяемым радиусом падения или путём падения. При этом инверсионное равенство радиуса пути падения дуге земной окружности соответствует понятию одного радиана и означает срединное звено пространственно-полевого перехода в структуре падения, как объёмного полевого преобразования. А то, что инверсионный радиус падения становится длиной окружности, может быть только при условии образования радиуса падения этой окружностью, как уже перпендикулярно развёрнутой к наблюдателю и по отношению к инверсионному радиусу.

Этим инверсионное тождество «R≡2πR» означает как раз радианный поворот «пи/2» в пространственно-полевом переходе. По этой причине путь падения с высотой уменьшается уже не в два раза, а в «4пи» раза (2*2пи) от ожидаемого расстояния в виде движения в нашем массовом пространстве (т.е. подобном движению качения ядра или мяча по поверхности). А значит, в «2пи» раза уменьшается и линейная скорость падения по отношению к формуле «h=g*t2/2», применяемой старой физикой для всех высот падения. При этом скорость падения, заметим, из-за поворотности полевого пространства проявляется только при контакте тела с опорой.

4. Взаимно-центрический смысл третьего закона Кеплера и полевая структура левитации.

Итак, длина траектории падения с больших высот через контурную величину заряда поля силы тяжести «g0» записывается, как «h=g0*t2/4». Выражение же «4пи» означает квадрупольный вид поля силы тяжести, подобный и структуре магнитного поля (как воспринимаемого нами магнитного поля в виде уже окружного объёма) с тем отличием, что магнитное поле является в этом случае одно-центровым, а поле силы тяжести (поле весовой гравитации) имеет взаимно-центрическую или инверсионную структуру, переходящую в поле планетного вращения.

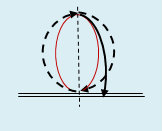
С увеличением высоты образование радиуса падения перпендикулярно к нему развёрнутой полевой окружностью, как сферической полевой окружностью (обозначенной на рис. ниже красным цветом), приводит к всё большему искривлению радиуса падения в параболический вид, что показано на рисунке. Такой полевой инверсией объясняется и параболическая траектория, например, снаряда при выстреле. И на высоте около 160 км. путь падения, воспринимаемый дугой земной окружности, окончательно переходит в окружность с радиусом, примерно равным радиусу Земли (плюс высота в 160 км.). На полевом же уровне радиус падения становится полуокружностью, чем образуется уже полная окружность (на рис. обозначена штриховой линией). Этим прекращается падение, обозначая границу поля силы тяжести, и начинается орбитальное вращение, объясняясь тем, что высота границы поля силы тяжести образуется высотой около 40 км. над поверхностью Земли окружного радиуса Земли (считаемого «барицентром» в гелиоцентризме), как сферического учетверения этого расстояния (о чём см. дальше).

Это значит, что постоянное (с увеличением высоты) искривление радиуса падения образующей его (и перпендикулярной к нему) полевой окружностью на высоте около 160 км. приводит к его инверсии в полуокружность, чем возникает уже полная полевая окружность с обратным вращением (см. рис. ниже). А этим полевая окружность, образующая радиус падения (показана в красном цвете), инвертируется уже во фронтальное положение к наблюдателю, а полевая полуокружность становится перпендикулярной к наблюдателю контурной орбитальной окружностью. Т.е. инверсионный радиус падения на высоте около 160 км. полностью растягивается в полуокружность, чем становится явно проявленной (в её фронтальном виде) и полевая окружность в виде инверсионного тождества «R≡πR≡2πR». В связи с этим происходит новая полевая инверсия, проявляющая поле планетного вращения, как образование полного контурного вращения вокруг земной поверхности и уже - в плоскости, перпендикулярной к наблюдателю. И образуется такое орбитальное вращение полевой окружностью с диаметром, равным высоте до поверхности Земли, которую в этой связи можно назвать «высотной» окружностью.

А поскольку орбитальная контурная окружность всё также должна образовываться синхронно (за то же время), что и «высотная» частотная («чисто» полевая) окружность, то этим и объясняется, что на низких орбитальных высотах оборот совершается всего за час с небольшим. При этом высотная окружность как бы стягивает орбитальную окружность с каждым оборотом, снижая её. Всё это наглядно показывает, что все проявления поля весовой гравитации – это инверсии полевой структуры, а не некое притяжение.



На высоте же геостационарной орбиты (около 36 тыс. км.) уже и «высотная» окружность также становится орбитальной окружностью, перпендикулярно направленной к самой орбите. Этим прекращается снижение или стягивание орбиты «высотной» полевой окружностью, которая вместе с орбитальной окружностью становятся частотной и контурной образующей полевой сферы планетного вращения. В связи с этим пространственные объёмы, образуемые выше 36 тыс. км. над земной поверхностью, можно назвать сферическими объёмами, от высоты 36 тыс. км. до границы поля силы тяжести – переходными пространственными объёмами, а от поверхности Земли до границы поля силы тяжести (точнее, поля силы падения) образуются окружные полевые объёмы.
То, что на полевом уровне радиус падения на границе поля силы тяжести (силы падения) становится полуокружностью и преобразуется этим в полную полевую окружность с обратным направлением, и вообще факт образования радиуса падения полевой окружностью означает возможность другой инверсии. Это преобразование радиуса падения в радиус выталкивания, как результат полевого поворота «?и» полевой полуокружности падения вокруг вертикальной оси.

Иными словами, приведённая полевая структура образования пути падения объясняет факты инверсии поля весовой гравитации, как например, аномалии течения в иных местах жидкостей вверх (см. 5, стр.104). Приведённой инверсией полевой полуокружности падения в полуокружность выталкивания объясняется и движение вулканической магмы вверх из-под мантии Земли. Т.е. под земной мантией идёт именно такая инверсия поля весовой гравитации в нижнее поле силы тяжести (см.5, стр. 122).
Поворотная инверсия полевой полуокружности падения обозначает и структуру левитации, как преодоления силы тяжести. Это значит, что образование вокруг тела полевой сферы, обратно развёрнутой на величину «пи/2» вокруг вертикальной оси относительно поля силы тяжести прекращает действие этого поля, а полны поворот на величину «пи» вызывает обратное движение вверх относительно земной поверхности. Такой разворот в виде преобразования молекулярных полевых объёмов прослеживается на примере поднятия газов. На основе инверсионной структуры движения падения указанный пространственно-полевой переход в последовательности его постоянных преобразований в начальном виде можно выразить образованием взаимно-центрического сопряжения двух сферических объёмов, что и образует исходное солнечно-земное вращение (и, например, лунно-земное вращение).

И проявляется очевидность такого вращения образованием смены времён года на Земле. Затем это сопряжение в нашей полевой фазе пространства переходит во взаимно-центрическое сопряжение сферического и окружного объёмов пространства, что выражается в дипольном или восьмеричном полевом образовании. Равенство же отношений сферического и окружного объёмов пространства, образованных каждой планетой, означает обращение взаимно-центрического вращения вокруг центра окружного объёма, что и образует окружной центр взаимно-центрической системы.
Обращение взаимно-центрического вращения вокруг центра окружного объёма означает, что окружной центр (воспринимаемый в гелиоцентризме неким «барицентром») образуется рядом с ведущим или с доминантным телом в системе. При этом наличие магнитного поля, – это один из основных признаков ведущего или доминантного тела во взаимно-центрической системе. Кроме того, вращение планеты и звезды (в составе их взаимно-центрической или двойной системы) вокруг окружного центра и образует их вращение вокруг оси.

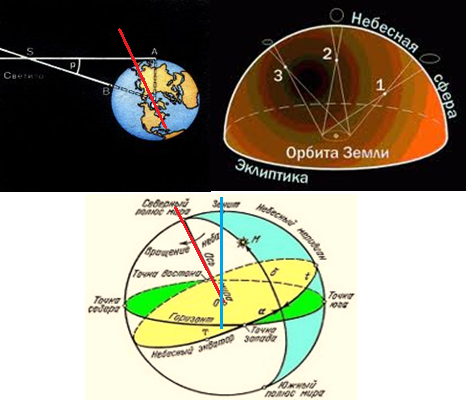
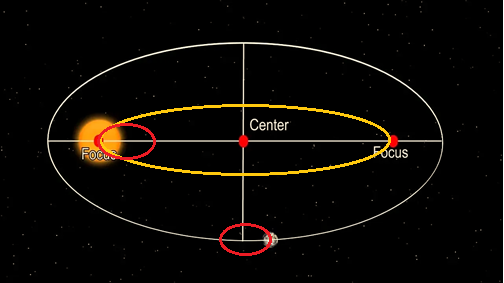
А обращение взаимно-центрической орбиты вокруг окружного центра, находящегося рядом с ведущим телом в двойной системе как раз и образует восприятие или иллюзию двухфокусной эксцентричной орбиты (относительно ведущего или доминантного тела) по первому закону И. Кеплера из-за полевого тяготения в нашей массовой фазе пространства к одно-центровому вращению. Этим эллиптические координаты (см. рисунок ниже слева) можно назвать искривлением исходной взаимно-центрической полевой окружности по причине образования одинарного центра окружного объёма нашего массового полевого пространства. Наглядность такого инверсионного вращения проявляется в двойной системе Плутона и Харона (см. рисунок ниже справа).



Первое требование Н. Коперника можно понимать и так, что не может быть вообще какого-либо одного центра для всех планетных орбит. Этим и наблюдаемая конфигурация планет – это иллюзия восприятия одно-центрового планетного вращения. Действительно, полное вращение (в радианном выражении «2пи») вокруг точки, как центра окружности, или вокруг одной оси невозможно в свободном пространстве космоса. Ведь нельзя закрепить в свободном полевом пространстве точку или ось. Потому и в космических наблюдениях видят вращения двойных систем, а не вращения одного тела вокруг другого. Но, исходя из неверного понимания гравитации или тяготения притяжением назначают при этом опять один (причём и одинарный) центр для двойных систем в виде некоего «барицентра» или «центра масс», нарушая этим требование Н. Коперника.
Более того, не берётся в расчёт то, что обозначение у этой системы центра тяжести (чем и есть фактически «центр масс») абсурдно в невесомости космоса.

Абсурдно потому и назначение «центром масс» точки, находящейся внутри космических тел (например, внутри тела Земли), поскольку это исключает возможность их вращения вокруг оси. Т.о., даже полевая структура падения с образованием дуги падения полевой окружностью, длина которой равна «дуговому» радиусу (полевому радиусу в виде дуги), проявляя этим иллюзию некоего «равноускоренного» падения, говорит о несоответствии наблюдаемой нами картины мира её полевой реальности. Отсюда и иллюзия конфигурации планет в виде их отдельного от Земли захода за Солнце, и, например, иллюзия вращения удалённых звёздно-планетных систем (считаемых и галактиками, и некими двойными, и тройными звёздами), как их годового вращения.

Литература и интернет-источники:

1. Занимательное различение (Искажение нашего времени). Книга 1-я. Различение физики и астрономии. Филиппов В.В. 2010-2013.

2. Частотно-контурное строение вещества и его квантовый переход. (Книга 4-я теории различения). Филиппов В.В.2014.

4. Советский энциклопедический словарь. Гл. ред. А.М.Прохоров. - М.: Сов. Энциклопедия, 1983.

5. Взаимно-центрическое тяготение пространства (Космофизика теории различения), Том I (Книга 5-я Теории различения). Филиппов В.В. 2014-2017.