|
Меню сайта
Категории
Новые статьи
Новое на форуме
Опрос
|
Точки Лагранжа и сферы Хилла, как свидетельства взаимо-центризма.
Предисловие. Всемирный закон гравитации можно назвать все-космическим законом взаимно-центрического вращения. Напомним, что Ньютон выявил зависимость убывания ускорения свободного падения на Земле до показателя центростремительного ускорения в орбитальном вращении Луны от квадрата расстояния между Луной и Землёй. Этим не только ускорение свободного падения отождествляется с зарядом вращения (центростремительным ускорением в традиционном восприятии). При этом устанавливается и общее поле лунно-земного планетного вращения, имеющее общий заряд вращения.
И квадратичная зависимость изменения полевого заряда вращения от расстояния между точками полевых орбит может означать в плоском виде (в нашем окружном пространстве) только взаимное вращение этих орбитальных точек вокруг друг друга. Только в этом случае может происходить сопряжение расстояний в виде радиусов между орбитальными точками.
Графически такое вращение обозначается спиралью, которая имеет свойство быть направленной, как на скручивание, так - и на раскручивание. Т.о., всемирный закон гравитации устанавливает не взаимное линейное притяжение космических масс, как бы волшебным образом приводящее к всеобщему вращению планет на их орбитах, причём - на стабильных орбитах. Всемирный закон гравитации или тяготения устанавливает пространственное или вращательно-полевое тяготение.
Тяготение же линейного свойства в виде силы падения, а затем и силы тяжести является уже не всемирным тяготением, а - его особым проявлением, как поля силы тяжести, возникающего вокруг массивных космических объектов. Это поле относится к переходному пространству расслоений (в стандартной модели) или к сферическо-окружному переходу. Здесь контурные силовые линии поля перпендикулярны наблюдателю. будучи направленными к центру планеты. Но за внутренним уровнем земной коры таковыми становятся уже частотные силовые линии, обратные к контурным (чем и объясняется подъём вулканической магмы). Потому можно сказать, что сила тяжести - это проявление пространства расслоений или сферическо-окружного пространственного перехода вокруг массивных космических тел, а никак не все космическое явление.
Общее поле лунно-земного вращения также в силу взаимо-центризма образуется отдельными планетными полями Земли и Луны, в центре которых (и за счёт которых) они и вращаются. Таким фактом объясняется и постоянство планетных орбит. Взаимно-центрическое вращение устанавливается, естественно, и в астрономическом наблюдении. Но из-за восприятия гравитации лишь короткодействующей силой притяжения (не отличаемой, кстати от силы тяжести) между массами, точнее - между их наружно молекулярными оболочками, определяют отсутствующее в природе некое вращение вокруг общего центра масс (не различаемого фактически от общего центра тяжести).
Уже одно назначение центра масс, подобного центру тяжести, двум совершенно отдельным телам, не связанных никакими видимыми связями, и находящимися в невесомости, является абсурдным. При этом назначают вращение каждому из двух тел вокруг такого "центра масс". И на то, что при допущении такого вращения вокруг точки, якобы лежащей на уровне около 1600 км. под поверхностью Земли, естественно нарушается условие для смены времён года, просто не обращается внимание. И это происходит потому, что традиционное восприятие не знает дополнений к законам Кеплера о взаимо-центризме.
Наблюдая же явное взаимно-центрическое звёздно-планетное вращение в астрономических наблюдениях, исходят из ложной концепции гравитации, как проявления силы тяжести,
и - из вращения космических тел вокруг центра тяжести (отсутствующей в космосе). Потому и взаимно-центрическое вращение звёзд и их ключевых планет (подобное солнечно-земному вращению) определяют некими двойными звёздами. Нахождение же центра взаимного вращения там, где он и должен быть: в центре между телами, считают в восприятии вращения вокруг не существующего в свободном космическом пространстве "центра масс" свидетельством огромной массы второй звезды, как некоего "белого карлика.
Планетная сфера или поле планетного вращения.
То, что вокруг любого космического тела образуется поле или сфера его вращения свидетельствуют факты превышения периода вращения планет над периодами вращения их спутников. Например, спутники Марса Фобос и Демос вращаются почти в три раза быстрее Марса, также и некоторые спутники больших планет имеют меньший орбитальный период по сравнению с периодами вращения самих планет.
Такое обстоятельство двух типов вращений может быть только в случае наличия и двух источников вращений, а точнее – при инверсии структуры одного планетного вращения. Согласно концепции взаимно-центрического планетного вращения планетная сфера планеты совершает движения качения по планетной сфере другой планеты или звезды, образуя взаимно-центрическое вращение. А образуемая таким образом единая сфера взаимно-центрической системы совершает движение качение или по планетной сфере, или – по сфере другой (предшествующей ей) взаимно-центрической системы.
Угловой, частотный или сферический период вращения планетной сферы равен и периоду вращения планеты. Аналогично и период вращения крайних точек цельного тела наподобие шкива равен периоду вращения центральной части тела. В традиционном же восприятии рассматривают совершенно абстрактные скорости точек поверхности тела (например, того же шкива), называя окружную скорость шкива (как его крайних точек) некоей линейной скоростью.
В традиционной физической теории и само вращательное движение определяется, как движение твёрдого тела, при котором две его точки, через которые проходит ось вращения, остаются якобы неподвижными. Но ведь всем известно, что только при вращении вала может вращаться и шкив, закреплённый на нём. Потому при вращении тела вращается, естественно и его ось вращения, а значит, вращается и сама пространственная структура.
Образование поля планетного вращения, а вместе с ним - вращения планеты (и самого её становления) спиралеобразно (в виде частотных силовых линий) исходит из центра планеты. Подобно и вращение цельного тела исходит из его центра. Проявляется же поле планетного вращения (вращением спутников и полем силы тяжести) обратным или инверсионным движением спирального схождения контурных силовых линий.
В таком движении период вращения объектов в поле планетного вращения уже зависит от радиуса их орбиты, т.е. – является уже окружным периодом. Скорость же вращения объектов определяется гравитационным зарядом поля планетного вращения (называемого в традиционной теории ускорением свободного падения).
И у Земли, гравитационный заряд для поля силы тяжести которой можно принимать эталонным или исходным (на фоне отсутствия в природе некоей гравитационной постоянной, как абсурда назначения постоянной величины для универсального или всеобщего, непостоянного взаимодействия), окружная скорость вращения космических объектов получает максимальную величину в виде первой космической скорости по формуле вращения «V= √πR*g0», исходящей из частотного значения величины «g» (без числа «пи). Т.о., в случае периода вращения планеты вокруг оси имеют дело с угловым или частотным периодом, зависящим от окружной скорости крайних точек планетой сферы, а значит, - от её размера и – от самой интенсивности её вращения.
В случае же вращения тел на планетной орбите имеют дело с окружным или контурным периодом вращения, зависящим от радиуса орбиты и от заряда поля планетного вращения. Этим и объясняется то, что спутники на малой высоте от планеты опережают её суточное вращение.
Но это не значит, что все тела, имеющие одинаковую орбиту, будут вращаться в поле планетного вращения с тем же периодом. Дело в том, что тела на планетной орбите также стремятся получить вращение вокруг оси. А масса тел (как их объём и плотность, но не как вес в традиционном восприятии), влияя на скорость образования их планетных сфер, влияет и на скорость их орбитального вращения.
При этом естественные спутники (вроде Фобоса и Деймоса) вращаются на орбите в их собственных планетных сферах, имеющих (согласно принципам взаимо-центризма) обратное или дипольное направление образования по отношению к вращению планеты вокруг её оси. В связи с этим поле или сфера планетного вращения спутника образует с планетной сферой спутника стабильное дипольное или восьмеричное образование.
Этим и объясняется тот факт, что они не увлекаются спиральными контурными линями поля планетного вращения, переходящими в силовые линии поля силы тяжести, образуя постоянные орбитальные окружности.
Кроме того, в связи с этим спутники вроде Фобоса и Деймоса, как и Луна, фактически не имеют вращения вокруг оси. Потому они и обращены к планетам всегда одной стороной. В таком вращении спутников Марса и больших планет вокруг них, вращение спутников вокруг оси, проходящее всегда синхронно с вращением планеты вокруг оси, лишь видимо обозначается вследствие их орбитального вращения вокруг планеты в положении дипольного соединения их планетной сферы с планетной сферы самой планеты (см. на рисунке ниже).
При этом спутник находится как бы в центре кармана своей дипольной сферы (обратного крыла контурной восьмёрки), увлекаясь вместе с ним в обращение вокруг планеты. Потому вращение спутника вокруг оси, синхронное с вращением планеты вокруг её оси – это лишь следствие такого орбитального вращения
Но Луна образует с Землёй взаимно-центрическое вращение (о чём речь дальше), имея постоянное положение своей оси в пространстве и вращаясь вокруг Земли в обратную сторону, являясь этим планетой, а не спутником. Потому отсутствие её вращения вокруг оси (проявляющееся либрацией) объясняется не синхронным взаимно-центрическим вращением Луны и Земли или одновременным образованием Землёю (как ключевой или начальной планетой) взаимно-центрического вращения с Солнцем. Вследствие этого планетная сфера Земли препятствует вращению планетной сферы Луны.
Спутники же вроде Фобоса и Деймоса обращены их осью всегда в сторону планеты, чем и являются именно спутниками. А вот менее массивные тела не образуют собственное поле планетного вращения, вращаясь контурными спиральными линиями поля планетного вращения в том же направлении вокруг оси и приближаясь этим к планете (в безусловном виде - после стационарной по отношению к планете орбиты).
Исходя из этого, можно сказать, что естественные спутники планет вращаются в центре их планетных сфер снаружи контурных силовых спиральных линий самой планеты. Потому эти силовые линии становятся устойчивыми окружностями орбит планеты. Малые же тела вращаются в центре их гравитонных сфер (как их наружно-молекулярных оболочек) изнутри силовых спиральных линий сферы вращения планеты, чем и увлекаются к планете вплоть до начала её поля силы тяжести, где переходят в падение.
Исходя из взаимно-центрической пространственной структуры, получается, что для выявления действительно существующей схемы планетного вращения необходимо исходить из второго дополнения Теории различения к законам Кеплера, говорящего о том, что и все планеты и звёзды совершают между собой взаимно-центрическое орбитальное вращение.
Кроме того, и закон всемирной гравитации, как зависимость гравитационных вращательных зарядов космических тел и полей вокруг них, от квадрата расстояния между телами, означает именно их сопряжённое или взаимно-центрическое пространственное вращение. Иными словами, обозначать схемы планетных и планетно-звёздных вращений необходимо не исходя из взаимодействия космических масс (отрывая вещество от пространства), а логичным образом – из структуры пространственного вращения, несущего и планетно-звёздные вращения.
Наиболее наглядно взаимно-центрическое вращение на примере системы двух малых планет из Плутона и Харона. Дело в том, что с периодом примерно в 6,4 суток происходит и вращение этих планет вокруг их осей, и – вращение Харона вокруг Плутона, который в диаметре около трёх раз меньше Плутона и вследствие этого воспринимается его спутником.
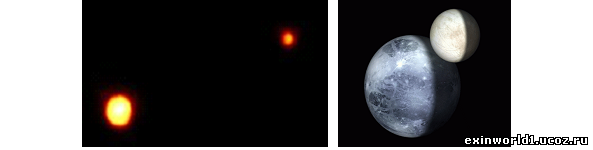
Такое тройное совпадение, естественно, никак не может быть случайным. И, поскольку традиционная астрономия не рассматривает взаимно-центрическое вращение, то её версия «приливного торможения» Харона, не может объяснять причину указанного совпадения, ограничиваясь лишь констатацией фактов.
При этом, рассматривая лишь вращение Харона вокруг Плутона, считают, что и Плутон, и Харон всегда оба обращены друг к другу одной и той же стороной, вследствие чего они должны висеть на небосклоне друг друга. А такая космическая неподвижность также не реальна. Кроме того, в рассмотрении обращения лишь Харона вокруг Плутона не понятна причина вращения Плутона вокруг оси, поскольку традиционная астрономия выявила и его обращение, но не вокруг Харона, а - вокруг абсурдного барицентра или центра масс.
Потому в действительности и Плутон, и Харон вращаются вокруг друг друга в одном направлении в центре их равновеликих планетных сфер или полей и за счёт их. В таком вращательном движении, которое можно рассматривать качением сфер вокруг друг друга, период вращения Плутона вокруг его оси всегда будет равен периоду обращения вокруг него Харона или совпадать с ним, поскольку этот период равен и времени обращения Плутона, совершаясь в течение его.
Во взаимно-центрическом вращении Плутона и Харона они имеют общую орбиту и находятся постоянно друг напротив друга. Но свойство любой окружности таково, что в диаметрально расположенных точках их общей орбиты однонаправленное орбитальное вращение Плутона и Харона получает разное направление. Потому они в действительности не находятся всегда друг напротив друга и не обращены друг к другу одной и той же стороной. Кроме того, в непосредственном взаимно-центрическом вращении направление вращения космических тел вокруг их осей должно получать разное направление (о чём см. ниже).
Т.о., астрономы, конечно, наблюдают взаимно-центрическое вращение в космосе, но, исповедуя абсурдную теорию гравитации в виде дальнодействующего притяжения масс, назначают двойной системе космических тел, находящихся в вакуумной невесомости, общую массу (а фактически – вес) с обозначением центра. При этом вращают вокруг этого «центра масс» не всю такую систему, а - каждую её часть, хотя центр масс должен предполагать объединение масс в общую массу, не говоря уже об абсурде раздельного вращения масс в их общей массе.
И наиболее абсурдно утверждение о таком взаимном вращении вокруг общего «центра масс» рассмотрение взаимно-центрического вращения системы Земля-Луна. Общий центр масс нашей двойной космической системы, вокруг которого вращаются Земля и Луна, назначают лежащим примерно на глубине 1600 км. от поверхности Земли.
Однако, во-первых, Луна имеет намного больший эксцентриситет её орбиты относительно центра Земли. Вращение же Земли вокруг этого центра якобы с тем же периодом, что имеет и Луна, естественно, никак не регистрируется, поскольку такого абсурдного вращения вокруг точки, значительно смещённой от центра Земли, и быть не может.
И, в-третьих, в этом случае смена времён года происходила бы в течение периода лунного обращения. Ведь ось вращения Земли, подобная оси гироскопа, при этом также должна совершать вращение вокруг этого несуществующего центра, изменяя этим и свою ориентацию относительно Солнца. А это – уже полный абсурд.
Взаимно-центрическое вращение, происходящее на Примере Плутона и Харона, показывает и взаимное поддержание такого вращения, чем и объясняется устойчивость планетного вращения. Дело в том, что направление вращения планетной сферы или планетного поля Харона (а значит, и самого Харона вокруг его оси) должно быть обратно по отношению к направлению вращения планетной сферы Плутона, что и выявляется в астрономических наблюдениях (10).
А потому вращение качением планетной сферы или планетного поля Плутона (находящегося в центре этого поля) по такой же сфере Харона поддерживается одинаковым моментом вращения и этой сферы, образуя с ней общий контур восьмёрки или диполя. В обратном порядке вращение сферы Харона в её движении качения по сфере Плутона таким же образом поддерживается и ею.
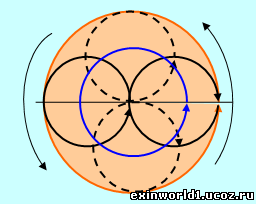 В результате и наблюдается общее строго синхронное вращение космических тел по общей орбите, (выделена на рисунке синим цветом) с диаметральным расположением тел на этой орбите. Орбитальное вращение планетных сфер, ограниченное окружностью, которую можно назвать орбитальным кольцом, действительно можно считать общей массой вещества, но не со смещённым центром масс (не различаемым от силы тяжести), а с центром вращения этой общей орбиты, как общей космической массы (не испытывающей, кстати, в вакуумном пространстве космоса и силы тяжести).
Если Харон сравнить с нашей Землёй, а Плутон – с Солнцем, то подобная схема вращения наблюдается и в солнечно-земном вращении. Отсюда становится ясно, что Харон движется по небосклону Плутона, а Плутон – по небосклону Харона, обозначая при этом вращения вокруг их осей, хотя они и расположены на их общей орбите ровно друг напротив друга.
И наблюдением с Харона будет восприниматься вращение Плутона вокруг него, а наблюдением с Плутона – вращение вокруг него Харона. Таким же образом были восприняты геоцентрическая и гелиоцентрическая планетные системы. В действительности же имеет место взаимно-центрическая планетная система.
Взаимно-центрическое планетное вращение происходит в космическом пространстве не только по причине взаимно-центрической пространственной структуры, но и потому, что имеет свойство регенерации. Дело в том, что физический (а не пространственно-метрический) центр вращения общей сферы взаимно-центрического вращения (как сферы системы Плутона и Харона) находится не между телами, а – одновременно в центрах космических тел, имеющих взаимно-центрическое вращение.
Ведь не только вращательное ускорение свободного падения на Земле (как заряд поля весовой гравитации, переходящий в результате пространственного поворота силовых линий поля в заряд поля планетного вращения) квадратично убывает по направлению к Луне. По закону симметрии пространства точно также заряд поля планетного вращения убывает и от Луны по направлению к Земле.
И, если бы Земля не совершала кроме взаимно-центрического вращения с Луной и взаимно-центрического вращения с Солнцем (как ключевая планета), то Луна подобно системе «Плутон-Харон» имела бы планетную сферу одинакового размера с земной планетной сферой, совершая и одинаковое с ней число вращений вокруг оси.
Однако взаимно-центрическое вращение системы Земля-Луна вследствие его протекания на фоне взаимно-центрического вращения системы Земля-Солнце приводит не к синхронному, а – к асинхронному взаимно-центрическому вращению. Вследствие этого отдельная планетная сфера Луны на внешнем или контурном уровне не регенерируется земной планетной сферой, а, наоборот, останавливается её вращение от земной планетной сферы (о чём речь дальше).
Вследствие этого Луна и не имеет вращения вокруг её оси, обозначая лишь либрацию (покачивание). Традиционное же утверждение о вращении Луны вокруг оси ровно за время её оборота вокруг Земли не соответствует действительности, поскольку из-за меньшего наблюдаемого лунного года в этом случае непременно поворачивалась бы и показывалась обратная невидимая с Земли сторона Луны.
Французский учёный конца 18-го века Ж. Лагранж правильно видел в явлении либрации Луны отсутствие её вращения вокруг оси. Но неверное восприятие гравитации или не восприятие (в силу того времени) сферическо-окружного перехода с перпендикулярным пространственным поворотом силовых линий планетного поля (при переходе от поля планетного вращения к полю силы тяжести) и рассмотрение в действительности отсутствующего дальнодействующего притяжения масс привели и к неверному восприятию наблюдаемого взаимно-центрического вращения.
Явление гравитации в силу этого приписали космическим телам, а не пространственной структуре поворотно-вращательного свойства. Всеобщее же пространственное явление взаимно-центрического вращения восприняли вращением вокруг некоего «центра масс». Напомним, что: 1) выражение для силы тяжести (m*g) посчитали и выражением силы падения, хотя процесс падения без учёта сопротивления воздуха не зависит от массы. Этим пространственно-полевой характер взаимодействия тел, определяемый вращательным ускорением свободного падения, обозначили силой тяжести.
2) Не выразили конкретного различия между массой тела и его весом, установив эталон для массы в виде веса. Это привело к тому, что образование силы тяжести назначили неким свойством массы и, в обратном порядке, массу тела обозначили, как некое свойство силы тяжести. 3) Короткодействующее взаимодействие наружно-молекулярных оболочек твёрдых тел посчитали взаимодействием их масс (не различаемых от их веса). Этим ввели некую гравитационную постоянную величину, имеющую отношение лишь к отдельному факту проявления гравитации.
4) Выражение для отсутствующего в природе взаимодействия масс (как внутрь направленных частотно-контурных образований) уравняли с выражением для силы тяжести. Этим и ускорение свободного падения, имеющее явно пространственно-структурное происхождение, стали считать следствием взаимодействия масс. 5) Внесли в третий закон Кеплера, совершенно не учитывающий массы космических тел, массовый коэффициент, как отношение сумм масс (не различимых от веса) для Солнца и рассматриваемых планет. Этим ввели ненужную погрешность в космические расчёты, как вращение вокруг смещённого относительно центра тел с большой массой «центра масс».
6) И, наконец, универсальность гравитации заключили в отдельном показателе интенсивности взаимодействия наружно-молекулярных оболочек твёрдых тел. В действительности же универсальность гравитации заключается в зависимости заряда вращения (центростремительного ускорения в традиционном восприятии) от квадрата расстояния между телами, как обозначения их именно взаимно-центрического вращения.
А ведь говоря о тяготении в космическом пространстве, И.Ньютон всегда подчёркивал о равном тяготении тел друг к другу или о двухстороннем выражении тяготения, что может быть только равным вращательным ускорением (вращательным зарядом в физике различения), как проявлением взаимно-центрической и поворотно-вращательной структуры пространства. Образование же силы падения, а затем (при контакте с опорой) и силы тяжести является уже односторонним выражением тяготения в результате сферическо-окружного пространственного перехода с перпендикулярным относительно наблюдателя разворотом силовых линий поля пространства.
Этот эффект заключается в том, что траектория падение тел до определённой высоты (19,62 м) всегда перпендикулярна к наблюдателю. Постоянное вращение космических тел является, таким образом, непременным проявлением пространственной структуры подвижного свойства. Восприятие же Ж. Лагранжа, оставшееся и до нынешних времён, гравитационные вращательные ускорения делает направленными не по спирали, а - всегда по прямой линии между двумя космическими телами, как обозначение притяжения тел, на каком бы расстоянии они не находились.
В традиционной астрономии устанавливается факт, что при удалении одного космического тела (менее массивного) от другого (более массивного) первое тело уже не падает на второе по прямой линии, а начинает вращаться вокруг него. Но приведённые пять искажений не позволяют воспринять причину начала вращения, что может быть только вследствие направления гравитационного ускорения по линии вращения, т.е. – по спирали.
И И.Ньютон, показывая, что под действием силы тяготения одно небесное тело может двигаться по отношению к другому по окружности (с разным эксцентриситетом) показывал этим и спиральный вектор силы тяготения. Традиционное же восприятие движение по окружности при наличии линейного вектора притяжения объясняет круглой формой планеты, соединяя форму и силу – два совершенно разных понятия.
Образование устойчивого вращения возможно только при двухстороннем выражении тяготения, т.е. - при обозначении взаимно-центрического вращения тел, а значит, - при выражении поворотно-вращательной структуры пространства. Т.о., традиционное восприятие Ж.Лагранжа лишь констатирует факт орбитальных вращений с образованием центростремительных ускорений, а начало вращений объясняет возникновением неустойчивого равновесия при разнонаправленном линейном взаимодействии тел, когда взаимное (линейно направленное) притяжение тел уравнивается. Но на то, что в этом случае вообще исключается движение (не говоря уже о вращении) попросту не обращается внимание.
Признаком же неустойчивого равновесия («волшебным образом» приводящего к орбитальному вращению) Ж.Лагранж и обозначил либрацию Луны. И, рассматривая орбиты вращения Луны вокруг Земли и Земли вокруг Солнца (в рамках гелиоцентризма) Лагранж рассчитал (исходя из третьего закона Кеплера с добавлением лишнего массового коэффициента) особые орбитальные точки, названные его именем.
В них (согласно традиционной физической теории) обнуляются или становятся равными не только силы неких линейных притяжений Земли и Луны или Земли и Солнца (в действительности отсутствующих после их стационарных орбит), но – и центростремительное орбитальное ускорение. На самом же деле в точках Лагранжа наблюдается лишь обнуление гравитационного пространственного заряда «g» (называемого ускорением свободного падения), относящегося к внутренней взаимно-центрической системе, как обозначение границ этой системы.
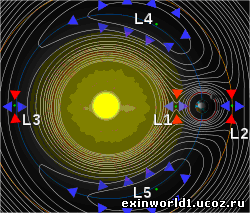
Кроме того, и закон всемирной гравитации (в его действительном выражении не через массы тел, а через гравитационные вращательные заряды структурно-пространственного происхождения) говорит именно о взаимно-центрическом планетном вращении. Потому и расчёты Ж.Лагранжа, относившиеся к системе «Солнце-Земля» и определившие его точки также говорят о взаимо-центризме (кроме точки «L3»). Точка же «L3» не соответствует действительности, как и сам гелиоцентризм, схема которого приведена на рисунке выше.
И в самом деле, приведённый рисунок указывает на явную асимметрию, что, естественно, невозможно в свободном пространственно вращении. Точки «L1» и «L2» примерно соответствуют границам общей лунно-земной взаимно-центрической сферы (поля), взаимодействующей с планетным полем Венеры и с взаимно-центрическим полем системы «Марс-Астероидная сфера».
Потому нахождение космических аппаратов в этих точках, как на стыках взаимно-центрических сфер, будет способствовать их стабильному положению в виде вращения в стабильной ориентации относительно и Земли, и Солнца. Эти точки соответствуют и точкам контакта в сферическом планетном вращении, в котором Марс, например, вращается почти на одном и том же расстоянии от Земли или также в стабильной ориентации относительно Земли и Солнца (о чём речь дальше).
Кстати, подобное взаимно-центрическое вращение кольцевой планетной сферы Урана с его астероидной сферой (о чём речь ниже) и приводит к эксцентриситету орбиты Урана, но – никак не возмущение его вращения Нептуном. Это говорит о том, что открытие Нептуна в 1846-м году означало торжество не гелиоцентрической системы (как традиционно считается), а на самом деле – взаимно-центрического планетного вращения.
И, поскольку всемирный закон гравитации является общекосмическим законом взаимно-центрического вращения, то и точки Лагранжа или орбитальные точки либрации рядом с земной орбитой обозначают не вращение Земли вокруг Солнца (точнее вокруг общего "центра масс", находящегося внутри Солнца), а - общую солнечно-земную орбиту. Повторим, что первая и вторая точки Лагранжа примерно обозначают точки контакта общей лунно-земной взаимно-центрической сферы с планетными сферами соответственно Венеры и взаимно-центрической сферы системы "Марс-Астероидная сфера".
Четвёртая же и пятая точки, лежащие в вершинах равнобедренного треугольника, образованного с одной стороны орбиты Земли вокруг Солнца, медианой, опущенной из этих вершин на линию, соединяющую Солнце и Землю как раз и обозначают взаимно-центрическое солнечно-земное вращение. Области вокруг этих точек соответствуют узловым точкам равноденствий в условиях взаимно-центрического вращения Солнца и Земли.
И, действительно, в случае гелиоцентризма по закону симметрии пространства такие же точки явно напрашиваются и с другой стороны орбиты Земли вокруг Солнца, но этих точек нет. Потому симметричность может быть только в случае общей солнечно-земной орбиты при обозначении взаимно-центрической планетной структуры.
Те точки Лагранжа, которые обозначают нахождение космических объектов в них всегда примерно на одном и том же расстоянии от Солнца и Земли, относятся в связи с этим к сферическому или к внешнему космическому пространству (через пространство расслоений), чем и объясняется размытость областей вокруг точек. Третья точка Лагранжа, обозначая гелиоцентризм, естественно, не соответствует действительности.
Третьей точкой можно отнести к области взаимного солнечно-земного центра, где также обнуляется гравитационный заряд «g» взаимно-центрической системы. Но здесь не только сохраняется постоянное расстояние от Солнца и Земли, но – и постоянное положение относительно солнечно-земной плоскости эклиптики, совершающей взаимно-центрическое вращение с другими (последующими) взаимно-центрическими системами. Такое обстоятельство также не различается традиционной астрономической теорией.
В точках же L4 и L5, соответствующих узловым орбитальным точкам равноденствий в условиях взаимо-центризма, сохраняется уже только постоянное положение относительно солнечно-земной плоскости эклиптики, поскольку через эти точки совершается синхронное орбитальное вращение Солнца и Земли. Кроме того, в симметричном порядке необходимо обозначить и две другие дополнительные точки - шестую и седьмую, как точки контакта общей планетной сферы (поля) системы "Солнце-Меркурий" с планетной сферой Венеры и с взаимно-центрической сферой системы "Марс-Астероидная сфера".
Это означает и то, что в сферическом или внешнем пространстве через космическое переходное пространство расслоений совершается перпендикулярный поворот "пи/2". В окружном же или во внутреннем, непосредственно наблюдаемом нами пространстве совершается окружное вращение взаимно-центрических систем космических тел вокруг общего солнечно-земного вращения. И происходит такое движение в силу пространственной структуры поворотно-вращательного свойства.
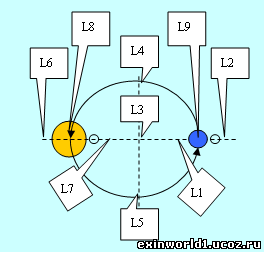
Приведённое выше размещение точек Лагранжа уже отвечает требованиям симметрии пространства, подчёркивая и истинность взаимо-центризма. Поскольку на приведённом рисунке области точек L4 и L5 соответствуют узловым орбитальным точкам равноденствий, то необходимо обозначить и перпендикулярно к ним расположенные точки солнцестояний L8 и L9.
Т.о., во взаимно-центрической схеме планетного вращения появляются уже девять точек Лагранжа. Первая, вторая, шестая и седьмая точки обозначают постоянное расстояние находящихся в них космических объектов от Солнца и Земли и относятся к сферическому пространству. Третья точка обозначает, кроме того и постоянное положение относительно солнечно-земной плоскости эклиптики, относясь к переходному космическому пространству расслоений.
Четвёртая, пятая, восьмая и девятая точки обозначают уже только постоянное положение относительно солнечно-земной плоскости эклиптики, относясь к окружному или к внутреннему пространству. О наличие же планетных и взаимно-центрических сфер свидетельствуют в свою очередь так называемые сферы Хилла в традиционной астрономической теории (отрывающей планетное вращение от пространственной структуры).
Сферой Хилла или Роша там считается пространство вокруг астрономического объекта (например, планеты) в котором он способен удерживать свой спутник, несмотря на притяжение объекта, вокруг которого обращается сам (например, вокруг звезды). Также и спутнику назначается собственная сфера Хилла, и в её пределах любой объект будет стремиться стать спутником спутника, а не планеты.
Здесь линейно направленное притяжение объекта не различается от его вращения, хотя это, естественно, совершенно разные движения. А потому в теории гелиоцентризма, исходящей и из неверной теории гравитации, провозглашается тот абсурд, что «нахождение спутника в сфере Хилла какого-либо объекта не означает, что этот объект притягивает его сильнее, чем тот, вокруг которого он обращается сам».
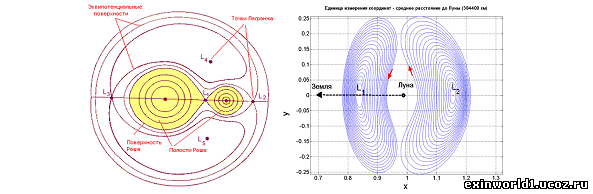
И, например, Солнце якобы притягивает Луну в 2,2 раза сильнее, чем Земля. Но вот почему она всё-таки вращается непосредственно вместе с Землёй, а не с Солнцем, понятно, остаётся без ответа, как и любой абсурд. Радиус сферы Хилла равен расстоянию до симметричных точек Лагранжа, например, - до точек L1 и L2, а значит, обозначает не что иное, как взаимно-центрическую сферу системы «Земля-Луна».
При этом в гелиоцентризме центр этой сферы для системы «Земля-Луна» совпадает с абсурдным «центром масс» этой системы, находящемся якобы внутри Земли. В действительности же он, как и во взаимно-центрической системе «Солнце-Земля», лежит посередине расстояния между объектами, в данном случае - между Луной и Землёй.
Это обстоятельство видно и по графику сферы Хилла, приведённому вверху справа, где точка Лагранжа для системы «Земля-Луна» находится фактически посередине лунно-земного расстояния. При этом взаимно-центрическую сферу системы «Земля-Луна», образованную вращением качения планетных сфер Луны и Земли вокруг друг друга, можно обозначить перехлёстом разнонаправленных орбит: орбиты Луны вокруг Земли (образуемой здесь в течение лунного месяца) и орбиты Земли вокруг Луны (образуемой в течение орбитального земного года).
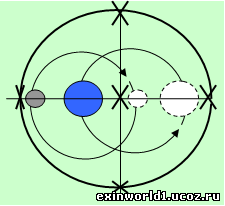
В такой внутренней взаимно-центрической системе, обозначенной не сферически или не качением планетных сфер вокруг друг друга (общей орбитой), а перехлёстом их отдельных орбит, можно обозначить уже только пять истинных точек Лагранжа: в центре системы, как в центре взаимно-центрической общей сферы вращения, и в четырёх узловых точках (обозначенных на рисунке крестиками). Две точки лежат на линии Землля-Солнце и две другие точки перпендикулярны им.
|
Категория: Космос | Добавил: viklehti (24.09.2014)
| Автор: Филиппов В.В.  
|
| Просмотров: 11256
| Источник статьи
|
|
|
Вход
Профиль
Понедельник 06.05.2024 17:20

Интересное
Поиск по сайту
Новости космоса на главной странице Яндекса.
Добавьте наш виджет, кликнув по картинке, и будьте всегда в курсе последних событий.
Чат Пульсар
Статистика
Онлайн всего: 21 Гостей: 20 Пользователей: 1
Нейтрино
|










