В чём же всё-таки смысл доказательства российским математиком Г. Перельманом гипотезы Пуанкаре, а главное – почему он отказался от миллионной награды и не выпустил статью, подводящую итог его доказательству? Вот как раз в последнем факте и кроется причина на первый взгляд странного поведения учёного.

Гипотеза Пуанкаре относится к топологии, к науке о геометрических фигурах и их свойствах, сохраняющихся при деформациях или преобразованиях фигур, идущих без разрывов. Изложенная Пуанкаре в 1904 году гипотеза утверждает, что все трехмерные поверхности в четырехмерном пространстве (в пр-ве с четвёртой осью), гомотопически (т.е. в их непрерывном преобразовании) эквивалентные сфере, гомеоморфны ей (преобразуются в неё). Проще говоря, если любая трехмерная поверхность чем-то похожа на сферу, то преобразующая её деформация всегда приводит к сфере. Вселенная по Пуанкаре подобна его трёхмерной сфере. И это вовсе не одно-центровая застывшая сфера, как воспринимается не полевой топологии, а сфера подвижная, а значит - полевая или октаэдрическая по теории различения, не имеющая стационарного и стабильного центра (см.1, стр. 234, 451). Вот потому и гелиоцентрическая модель старой (не полевой) астрономии согласно гравитации-притяжения вынуждена признавать, что «центр масс» или барицентр нашей планетной системы совершает спиральное движение, абсурдно пересекая даже наблюдаемое сферическое тело Солнца, что противоречит и самому гелиоцентризму.



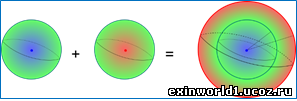
Трёхмерная сфера Пуанкаре в четырёхмерном пр-ве описывается именно в полевом движении (см. рис. выше), т.е. - подобием образования глобуса из двух сфер, формирующих северное и южное полушария, более того, и экватор, по которому как бы «склеиваются» эти сферы, - это также сфера. Две сферы, подобные северному и южному полушариям, образуют восьмеричную полевую фигуру или диполь. А соединение диполя в его движении через сферу, - это и есть, нечто иное, как исходное взаимно-центрическое полевое вращение, которое через пространственно-полевой переход, одновременно образует и фигуру тора, и стягивается затем в одно-центровую сферу. В плоском или во фронтальном виде это образует дифракционную картину, как дискретное восприятие спирального вращения. Т.е. в рассмотрении поворотной полевой структуры пространства теории различения – это взаимно-оболочковое вращение или вращение гравитонных сфер вокруг друг друга с одновременным движением этого вращения вокруг полевого окружного центра или гравитационного фокуса, что и воспринимается третьей сферой в виде фигуры тора (бублика).

Четвёртая ось четырёхмерного пр-ва и выражает собой «п-п» переход по теории различения, структурно обозначаемый (на фоне исходной магнитной частоты «10^6») из числителя постоянной Зоммерфельда и постоянной Н. Козырева в виде «πи/√2*10^6» (см. 2, стр.19, 44) и описываемый в виде спирали числом Фибоначчи (см. 4, стр. 275). Графически же четвёртую ось «πи/√2» в топологи теории различения можно представить в виде скрученного тора. Отсюда фигуру тора структурно можно обозначить в виде выражения «πи/√2». При этом движение по такой четвёртой оси означает не некое дополнительное движение (в виде некоего четырёхмерного гиперкуба), как представляется в употребляемой не полевой топологии, а - объёмное вращение по трём декартовым осям одновременно, что несколько подобно стереографической подвижной проекции тора (см. ниже). В подвижном полевом пр-ве теория различения потому рассматривает не неподвижную мерность, а его поворотность.



Поскольку не полевая топология из трёхмерной сферы Пуанкаре сразу делает одно-центровую застывшую сферу, стягиваемую в точку, то этим якобы доказывается и одиозная гипотеза «большого взрыва», несовместимая не только со здравым смыслом (в чём взорвалось, как получилось из взрыва постоянное и равномерное во времени вращение, а не разлёт осколков? и т.д.), но расходящуюся и с понятием пространства-времени (исходящем ещё от И. Ньютона), как подвижного само-формирующегося полевого образования. К тому же одно-центровые сферы нашего видимого мира, как представленные видимым нами веществом, составляют лишь около 5% от наблюдаемой вселенной.
Г. Перельман доказал гипотезу Пуанкаре попутно, когда доказывал теорему геометризации Тёрстена при помощи математического аппарата «плавной эволюции» из дифференциальных уравнений. Фигурой тора в доказательстве Перельмана как раз и «разрезается» любое «замкнутое трёхмерное многообразие». Уравнения «плавной эволюции» можно назвать дифференциацией на отдельные части «п-п» перехода, как поворота по четвёртой объёмной оси «πи/√2». Как раз по этой причине и из-за общей зеркальной симметричности полевого пр-ва «плавная эволюция» с применением фигуры тора в переходе к трёхмерной сфере Пуанкаре и прошла успешно.

В реальности же идёт обратное полевой движение от сферического исходного пр-ва, выражаемого подвижным полевым объёмом «Vs» в виде квадрата периода (из различения третьего закона Кеплера) «Vs=Т^2», - через объёмный поворот по 4-й оси «п-п» перехода с образованием взаимно-оболочкового вращения и переходной фигуры тора – к одно-центровой сфере и шару, обозначаемым окружным или массовым объёмом «Vm=4/3πиR^3» (см. 1, стр. 237). Одно-центровой объём образуется сочетанием торов, как перпендикулярных друг к другу контурных и частотных полевых образующих (круговых слоёв). Этим общая структурная запись «п-п» перехода исходно магнитной частоты «10^6» получает вид: «(πи/2: πи/√2: πи)10^6/ (πи: πи/√2: πи/2)10^6». Полевой одно-центровой объём формирует фигуры уже видимого нам мира, включая и обычный (одно-центровой) октаэдр. При этом переход в одно-центровые фигуры уже не возвратный.

«Фишка» сочетания тора и одно-центровой сферы состоит в том, что, например, воздушный шарик легко преобразуется в различные фигуры, что показывают для детей в парке. Но сделать из него бублик (или тор) не получится. И наоборот, невозможно сделать из резинового бублика сферу, что показано ниже.


Это значит, что по их топологическим свойствам поверхности сферы и тора не «гомеоморфны», не преобразуются друг в друга. Тор, как и трёхмерная сфера Пуанкаре (в её исходном виде), не стягивается в одну точку. Одно-центровая сфера односвязная, стягиваясь в точку, тор же уже двух-связен. Получается, что не гомеоморфный сфере тор преобразует трёхмерные поверхности в четырёхмерном пр-ве в сферу. Не различение того, что обратное преобразование трёхмерной сферы Пуанкаре, причём, как именно полевой сферы без стабильного центра, в одно-центровую сферу идёт через фигуру тора и не позволило Г. Перельману составить статью, подводящую итог его доказательству.

Такое не различение привело и к другой формулировке гипотезы Пуанкаре, гласящей в сокращённом виде, что всякое только односвязное (не подобное тору) трёхмерное многообразие гомеоморфно трёхмерной сфере, хотя трёхмерная сфера по доказательству Г. Перельмана получается в его плавной эволюции трёхмерного многообразия как раз через тор. Об этом говорит и полый внутри конечный вид трёхмерной сферы, что в употребляемой не полевой топологии не может иметь объяснения. Получается, что употребляемая одно-центровая топология, как топология исходности видимого вещества (того что только ощущаем), не зная о состоянии полевой трёхмерной сферы без стабильного центра, получает сферу с одним центром через тор, хотя он и не может стать такой сферой. Это всё равно что получать одно число делением на другое, но которое не может стать первым.

Такой абсурд и стал причиной отказа Г. Перельмана от получения полагающейся ему высокой награды. Ведь с точки зрения математика такая награда уравнивалась с унижением: блестящее доказательство в рамках употребляемой топологии превратилось в полный абсурд. Его отказ от премии стал по сути протестом против довлеющей в научном обществе парадигмы «большого взрыва», т.е. - исходности видимого вещества (составляющего, напомним, лишь 5% от наблюдаемой вселенной), а не полевого пр-ва.

Литература и интернет-источники.

1. Зеркальный космос (Взаимно-оболочковая система мира с комментариями взаимо-центризма). Книга 6-я Теории различения. 2017-2019.
2. Частотно-контурное строение вещества и его квантовый переход. (Книга 4-я теории различения). Филиппов В.В.2014.

4. Взаимно-центрическое тяготение пространства (Космофизика теории различения), Том I (Книга 5-я Теории различения). Филиппов В.В. 2014-2017.