.

Вращение видимых нами тел происходит по окружности и по эллипсу, обозначая окружной объём. Исходное же пространственное вращение, поддерживающее физические поля, в том числе и поля или сферы планетного вращения, обозначает сферический объём. Потому и вращение сферическое или пространственное «4пиR» не равно вращению окружному «2пиR»,происходящему в мире наших пропорций.

Сферическое вращение, в структурной записи можно представить, как 4пиR:(2пиR)q(2пиR)k. Эта запись состоит из частотной «(2пиR)q» и - из контурной «(2пиR)k» образующей сферы, которые перпендикулярны друг другу (и, кроме того, перпендикулярно развёрнуты относительно друг друга). Именно такое сочетание и образовало размерность «м2» электрической сферы вращающегося (переменного тока) в различении опыта Р. Милликена (1), называемой в бытующем физическом восприятии зарядом.

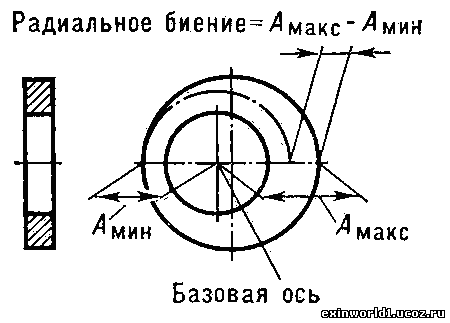
В связи с этим необходимо различать первый закон Кеплера, говорящий об эллипсоидном виде орбит космических тел. Эллипсоидный вид орбит искусственных спутников Земли, как и эллипс, образуемый из-за смещения оси вращения относительно геометрической оси (например, в виде радиального биения вращающегося цилиндра) относится к окружному вращению и, соответственно - к окружному пространству.



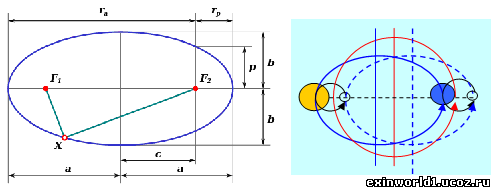
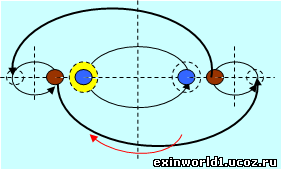
Этот эллипс имеет один фокус, означающий смещение оси вращения определённого тела относительно отсчётной оси. И только в этом случае можно говорить об эксцентриситете вращения тела. Первый же закон Кеплера обозначает уже два фокуса F1 и F2 эллипса (на рисунке ниже слева), относящиеся к вращению не одного тела относительно центра вращения в виде Солнца, как считается в традиционном восприятии.

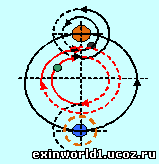
Первый закон Кеплера относится к взаимному вращению двух тел, обозначая их диаметральные положения в окружном вращении относительно центра эллипса, как пространственной оси вращения. И эта ось получает смещение относительно центра идеальной внешней взаимно-центрической орбитальной окружности (обозначена на рисунке справа красным цветом), которая образуется вращением внутренних взаимно-центрических вращений (в данном случае систем Солнце-Меркурий и Земля-Луна).

И общее взаимно-центрическое вращение двух тел относится уже к сферическому пространству. Т.о., эллипс, образуемый орбитой каждой планеты согласно первому закону Кеплера, означает окружное изображение сферического пространственного вращения, как вращения взаимно-центрического, причём - включающего внешнее и внутреннее взаимно-центрические вращения.

И, хотя, в традиционном восприятии обозначают задачу двух тел, но – рассматривая её без различения внутренних и внешних взаимно-центрических вращений, которые в свою очередь воспринимают вращением вокруг некоего «центра масс». Во вращении же одного тела относительно другого, как центра вращения, обозначается лишь один фокус, и это задача вращения одного тела.



И, действительно, эксцентриситет вращения космического тела вокруг другого тела, образующий эллипс относительно не центра эллипса, а – центра другого тела, относится к смещению одной оси вращения, как к смещению от центра идеальной орбитальной окружности. Это и наблюдается во вращении спутников планет и комет (относительно планет и Солнца).

Потому в случае гелиоцентризма каждая планета получала бы смещение в виде эксцентриситета орбиты только относительно Солнца, но – никак не относительно Солнца, как первого фокуса эллипса, и относительно ещё и другого фокуса. В связи с этим обозначение двух фокусов – это не что иное, как обозначение двух диаметральных орбитальных положений Солнца, что является следствием и внешнего взаимно-центрического вращения Солнца относительно планет, и внутреннего взаимно-центрического вращения планет (например, в виде лунно-земного вращения), как и самого Солнца в виде взаимно-центрической системы (причём тройной) «Солнце-Меркурий».

Исходя из этого, и центр наблюдаемого вращения планеты – это не Солнце, а взаимно-центрический центр солнечно-земного вращения. А определяемый эксцентриситет такого взаимно-центрического эллипса (отношение «c/а» согласно рисунку выше) означает внутреннее взаимно-центрическое вращение планеты (идущее не относительно Солнца).

И такой взаимно-центрический эллипс орбиты планеты можно назвать следствием сферическо-окружного перехода, как искривления нашего пространства по отношению к исходному или к вакуумному пространству. Но исходная или пространственная орбита планет (на рисунке справа обозначена красным цветом), как её центральная взаимно-центрическая орбита (внутренняя и внешняя) образует идеальную окружность, о чём и свидетельствует второй закон Кеплера.

Такую орбиту можно назвать внешним вращением центра внутреннего взаимно-центрического вращения (что и нашло отражение в виде деферентов в теории Птолемея). Центр этой орбиты, как истинный солнечно-земной центр взаимно-центрического вращения и обозначает, например, своим перигелием относительно Солнца (0,587 а.е.) короткопериодическая комета Галлея.

Второй закон Кеплера говорит об образовании радиус-вектором планеты в равные промежутки времени равных сегментных площадей (несмотря на видимую или наблюдаемую эллипсность орбиты). Это обстоятельство и означает орбиту планеты (и звезды), как два её равномерные и синхронно идущие взаимно-центрических вращения (внутренние и внешние).

Т.о., наблюдаемые орбиты планет образуют эллипс вследствие их орбитального вращения, как одновременно идущего их внешнего и внутреннего взаимно-центрического вращения. При этом центр такого двухфокусного эллипса – это и есть взаимно-центрический центр внешнего вращения.

Потому, делая правильные расчёты для положения космических тел на небосводе, для планет получают неверные данные об изменениях их расстояний относительно Земли. И это происходит по причине не различения центра орбитального эллипса центром внешнего вращения планет.

Обозначаемый же в наблюдении эллипс больших планет вообще относится в действительности лишь к их внутреннему взаимно-центрическому вращению, причём – лишь в части этого вращения (о чём речь дальше). Кроме того, неверное представление получают и об орбитах нижних планет – Венеры, Меркурия и Луны (как также планеты).

В связи с этим и необходимо рассмотрение взаимно-центрического планетного вращения, дающего действительную картину движения планет. В традиционной же астрономии, естественно, верную схему наблюдения движения планет по небесной сфере переносят на неверную схему гелиоцентризма.



Согласно концепции частотно-контурного строения вещества теории различения (3) способ существования невидимой для нас пространственной структуры (в виде космического вакуума) – это и есть жизнь. Способ же существования нашей надвакуумной пространственной среды – это постоянно идущий сферическо-окружной квантовый переход (в виде пространственно-временной энтропии).

Именно этот процесс и образует воспринимаемость или реальность нашего мира (занимающего лишь около 5% от наблюдаемого крупномасштабного космоса), поддерживая и его существование. Такой квантовый переход прослеживается не только в различении тонких атомных (ядерных) структур и структуры пути падения тела, но, - и в формуле «h=gt²/2» (относящейся, к малой высоте падения - 19,62 м.), в том случае, если ускорение свободного падения (заряд поля силы тяжести) выразить через формулу оборотного маятника.

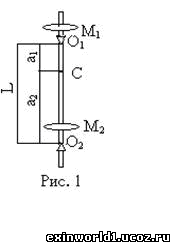
Оборотным маятником называют физический маятник с двумя остроконечными опарами - точками подвеса. Одна из опор является неподвижной, а другая – регулируемой. Оборотный маятник подвешивают попеременно на две опоры и регулированием подвижной опоры добиваются совпадения периодов колебания относительно каждой из опор, как осей колебания маятника.



Затем замеряется расстояние между опорами «L» и высчитывается величина «g» по формуле оборотного маятника g=4π²L/Т². Напомним, что такая формула ещё раз подтверждает структурно-пространственное происхождение традиционного понятия ускорения свободного падения, которое никак не связано с массой тел.

Кроме того, эта формула говорит и о величине «g», как о выражении вращательного заряда в физике различения (центростремительного ускорения в традиционной физике) в виде произведения «пи*(4пиR/Т²)» или «пи*gо», а не линейного ускорения, как приращения скорости (но употребляемого к тому же и в виде абсурда скорости изменения скорости).

Ведь выражение в формуле центростремительного ускорения «ац=V²/R» скорости «V», как именно вращательной скорости «2пиR/T» и даёт формулу оборотного маятника, где расстояние между оборотными опорами «L» выступает в виде радиуса окружности вращения «R». И, поскольку путь колебания маятника всегда есть частью окружности, то это обстоятельство означает не что иное, как гравитационную структуру пространства, в которой происходит взаимно-центрическое вращение двух равных колебательных окружностей, что и представлено на структурной схеме оборотного маятника ниже.



Формула «4пиR/Т²» (заряд вращения в физике различения), доказывается выражениями первой и второй космической скорости, как вращением соответственно по полуокружности (√πR*gо) и по полной орбитальной окружности со средним радиусом Земли (√2πR*gо). При этом напомним, что космические скорости, исходящие из неверного восприятия гравитации лишь силой тяжести, совсем не обязательны для вывода космических аппаратов на орбиту.

В связи с этим выражение «пи*(4пиR/Т²)», определяемое оборотным маятником, в его структурном рассмотрении означает сферический поворот на величину «пи» относительно взаимно-центрического центра вращения (обозначен крестиком на рисунке вверху справа) и – окружной вертикальный поворот «пи» также в вертикальной плоскости подвеса оборотного маятника с двумя опорами. В нашем же окружном пространстве (на рисунке вверху слева) в силу окружного вращения (2пиR), как в два раза меньшего сферического вращения (4пиR), происходит уже наложение колебательных окружностей оборотного маятника.

Вследствие этого (как наложения планетных сфер Земли и Луны друг на друга), кстати, и планетная сфера Луны влияет на Землю в виде приливов и отливов. Так вот, подстановка формулы оборотного маятника в выражение для пути падения тела с малой высоты даёт выражение «h=π*2пиR».

Потому в структурном рассмотрении путь падения тела и предстаёт в параболическом виде или приближенным к прямой линии, что спиральная окружность силовых или контурных линий поля планетного вращения, переходя в поле силы тяжести, получает горизонтальный окружной поворот «пи» в вертикальной плоскости, подобный повороту в схеме оборотного маятника. Это означает и то, что физические формулы необходимо рассматривать не только математически но (и в первую очередь) – структурно.

Таким образом, то, что величина «g» относится к вращению полевой пространственной структуры, но тела при падении тяготеют не вращательно, а линейно (как притягиваются и магнитные тела) означает сферическо-окружной пространственный структурный переход или поворот силовых линий планетного поля на величину «пи». Не различение такой гравитационной пространственной инверсии и приводит к абсурду рассмотрения планетного вращения через линейно направленную силу тяжести.

Структурная частота магнитного поля равна величине 106, свою частоту (происходящую, как и все структурные полевые частоты, от магнитной частоты, но уже, - как от частоты пространственной или исходной) имеет и поле силы тяжести. И равна она согласно физике различения величине ≈1,44*104 (3, стр. 290).

Частота же Фарадея (в различения числа Фарадея, как отношения контурной или молекулярно-связующей длительности 3,85*10-5 к размеру вращения атома), т.е. частота, контурно связующая молекулярные связи всех веществ тел (обратная величина 3,85*10-5) равна практически идентичной величине 2,6*104 «1/сек» (3, стр. 198). Этим и объясняется взаимодействие поля силы тяжести со всеми молекулярными веществами.



Напомним, что И.Ньютон в выводе закона всемирной гравитации использовал то обстоятельство, что вблизи поверхности Земли, т.е. на расстоянии около 6400 км. от её центра, ускорение свободного падения «g» (полевой заряд вращения в физике различения) составляет 9,81 м/сек2. А на расстоянии в 60 раз большем или уже у Луны это ускорение становится в 3600 раз меньшим. При этом 3600=602.

Исходя из этого, Ньютон пришёл, естественно, к верному выводу, что ускорение свободного падения убывает обратно пропорционально к квадрату расстояния от центра Земли. Означает это и то, что отношение «g» к центростремительному ускорению (заряду орбитального вращения) Луны согласно формуле центростремительного ускорения, как и оборотного маятника, обратно пропорционально указанному квадрату расстояния.

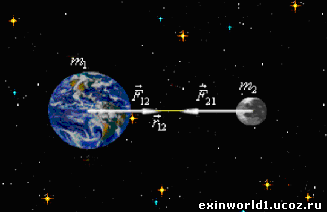
Но обратите внимание, что согласно формуле оборотного маятника «пи*(4пиR/Т²)» это отношение может быть пропорционально лишь первой степени радиуса, а значит – и первой степени расстояния от центра Земли, к тому же и не обратно, а прямо пропорционально, как к соответственно меньшему расстоянию от центра Земли. Потому вывод Ньютона обозначает никак не отношение центростремительных ускорений, а потому и не относится, естественно, и к полю силы тяжести Земли, и к её массе, как выражено на рисунке ниже.



Вывод Ньютона должен обозначать отношение тех же величин, но инверсионных или обратных к ним, как к размерностям центростремительных ускорений (зарядов вращений) «м/сек²». Потому рассмотренное отношение Ньютона касается не чего иного, как обозначения планетных сфер Луны и Земли в виде заряда их качения (что рассматривается в физике различения и не имеет аналога в традиционной физической теории).

Это отношение площади сферы качения пространственного объёма (образуемого, например, вращением обычным колесом) к периоду вращения (совпадающему с периодом образования указанной сферы): 4πR²/Т в размерности «м²/сек». В связи с этим величина «g», как поворотный заряд вращения поля силы тяжести (в виде произведения «пи*g0) численно и инверсионно равна обратному выражению заряда качения, как Т/4πR².

Такое инверсионное преобразование также является не чем иным, как выражением сферическо-окружного пространственного перехода в виде преобразования поля силы тяжести в поле планетного вращения. В структурной записи это преобразование (отношения величины «g» к центростремительному ускорению Луны «ац.») и выглядит, как g/ац: R²л/ R²з., или в виде квадрата отношения орбитального радиуса луны «Rл» и - планетного радиуса Земли «Rз» (как минимального радиуса качения её планетной сферы).

Дело в том, что центростремительное орбитальное ускорение Луны (заряд её орбитального вращения относительно Земли), как и ускорение свободного падения «g» (заряд поля планетного вращения близи Земли), относятся к разным периодам вращения. Для Земли – это длительность суток, для Луны – это период её орбитального вращения, как лунный месяц.

Заряд же качения для Луны и для Земли, численно равный соответственно «ац.» и «g», относится к одному и тому же периоду вращения в виде качения полевых сфер вокруг друг друга, как взаимного и синхронно идущего движения. По этой причине значения периодов и сокращаются в соотношении (Т/4πRз²)/(Т/4πRл²).

Потому согласно различению теоремы Э.Нётер (4, стр. 182) полевые заряды вращения, обозначая разную длительность вращения, относятся к открытой или к внешней пространственной системе и к окружному пространству. Заряды же качения, имеющие равную длительность, относятся к закрытой или к внутренней пространственной системе и к сферическому пространству (через переходное пространство расслоений, как через сферическо-окружной переход, имеющий зависимость от радиуса в отличие от сферического пространства, обозначаемого лишь угловой частотой).

Относительно уравнений Максвелла можно напомнить, что полевые заряды вращения, как и окружное пространство, относятся к оператору дивергенции «div». Полевые же заряды качения, как и сферическое пространство, и выражающее его переходное пространство, относятся к оператору вращения «rot».

В термодинамике есть и более конкретное обозначение окружного пространства, как пространства координат, и - пространства сферического (чрез воспринимаемое нами переходное пространство), как пространства импульсов. В связи с этим формула «g/ац: R²л/ R²з.» выражает не закон всемирной гравитации, а сферическо-окружной пространственный переход в полевых взаимодействиях.

Поскольку И.Ньютон не рассматривал в силу его времени пространственную структуру (не рассматривая и заряд качения), то и не мог оставить подобной структурной записи. Этим объясняется и то обстоятельство, что Ньютон, долгое время (в течение 21-го года!) не публиковал формулу закона всемирной гравитации.

Но и выложенная им формула включала произведение вовсе не масс тел, а – их гравитационных зарядов «μ». На основе этой формулы, как «(μ1*μ2)/R²» была выведена впоследствии и формула взаимодействия электрических зарядов Ш.Кулона. Этой формуле соответствует и взаимодействие свинцовых шаров в опыте Г.Кавендиша, где гравитационные заряды – это также вовсе не массы, а наружно-молекулярные заряды тел (заряды их наружно-молекулярных полевых оболочек), причём - определённого вещества (5).

Кроме того, и формула магнитного взаимодействия параллельных проводников с электрическим током величиной «I1» и «I2», расположенные на расстоянии «R» друг от друга в вакууме относительно участка проводника длиной «L» выглядит, как «(μ0/2π)*((I1*I2)*L*R)/R²» (здесь μ0 – магнитная постоянная). Ведь указанное взаимодействие относится к двум проводникам с током, а потому должно учитывать не длину участка одного проводника, а – всю площадь их взаимодействия.

Это означает, что и здесь имеет место обратная зависимость магнитного взаимодействия, как одного из проявлений гравитационных взаимодействий, от квадрата расстояний между центрами полевых образований, совпадающих с осью проводников. Т.о., несмотря на то, что тяготение или гравитация обозначена в теории А. Эйнштейна, как «универсальное взаимодействие между любыми видами физической материи», традиционная научная теория рассматривает гравитацию лишь в проявлении силы тяжести и некоего притяжения между массами.

И происходит это по причине не различения единой наружной или гравитационной полевой структуры пространства. Масса же – это уже не частотно-контурное, а чисто контурное, частотно застывшее и внутрь направленное полевое образование.

Формула Ньютона потому относится к взаимодействию близко расположенных тел (когда расстояния между ними меньше или сравнимы с их размерами). В связи с этим нельзя и вести речь о некоей единой формуле закона всемирной гравитации. Это следует и из самого определения гравитации, как фундаментального всеобщего взаимодействия.

Можно вести речь лишь о единой гравитационной или о наружной силовой пространственной структуре вращательного взаимно-центрического и поворотного свойства. Потому и закон гравитации Ньютона, как и его три закона, следует выражать в истинной формулировке, а именно – как обратную зависимость гравитационных пространственных взаимодействий от квадрата расстояния между центрами полевых (подобных сфере) образований вокруг тел.

При этом такая зависимость обозначает не что иное, как взаимно-центрическую структуру гравитации, как проявления наружных силовых полевых взаимодействий.



Попятное движение планет имеет, хотя и невразумительное, но объяснение привлечением разных орбитальных скоростей планет, что явно не стыкуется с петлеобразным движением Марса. Это движение имеет отношение к проявлению обратного направления внутреннего взаимно-центрического вращения Марса с Астероидной сферой наблюдением с Земли, имеющей подобное вращение с Луной. Постоянство же положения осей планет относительно звёзд не получает вообще объяснения в теории гелиоцентризма, поскольку есть следствием именно взаимно-центрического вращения планет.

Действительно, ось гироскопа сохраняет постоянство её положения в пространстве, но – только при линейном перемещении, исключая вращение. Ведь сохранение начального направления относительно центра вращения при его начале означает сохранение такого же направления и в диаметральной точке окружности вращения или орбиты при совершении вращения на величину «пи» или на 180 градусов.

А такое направление относительно пространства или относительно внешне неподвижных звёзд означает поворот на величину «пи» или на 180 градусов, т.е. – не сохраняет постоянства. Этим и объясняется тот факт, что орбитальным спутникам приходится принудительно поворачивать плоскости солнечных батарей по направлению к Солнцу.

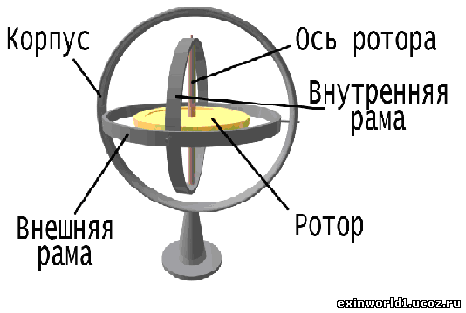
Ось планет, как и ось вращения Земли, всегда параллельна самой себе, т.е. сохраняет своё положение в диаметрально противоположной точке орбиты, чем и обеспечивается смена времён года. Схема гироскопа подобна внутреннему взаимно-центрическому вращению (например, Земли с Луною).

При этом взаимное качение планетных сфер вокруг друга, идущее в сферическом пространстве, в схеме гироскопа, отражающем окружное пространство, становится перпендикулярными друг другу внешней и внутренней рамой, соответствующими контурной и частотной образующим сферы.



Постоянство же положения оси вращения земной оси относительно звёзд обеспечивается уже внешним взаимно-центрическим вращением с Солнцем (через планетную сферу Венеры). Т.о., принцип постоянства положения планетной оси относительно звёзд может быть соблюдён лишь в условиях взаимо-центризма.

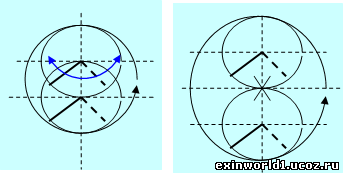
И, действительно, вращение гироскопа (или нескольких гироскопов, но, - как задачи вращения для одного тела) вокруг какой-либо оси не обеспечивает постоянства положения их осей относительно звёзд, поскольку правое положение оси в одной части окружности сменяется на левое положение в диаметральной точке окружности, что и изображено на рисунке внизу слева. И это происходит по причине поворота на величину «пи» (180°) вместе с гироскопом (телом) и самой пространственной структуры (что можно воспринять в повороте листа бумаги на просвет), как поворота в окружном пространстве.



При одновременном же повороте осей двух гироскопов в сферическом пространстве (как задачи именно вращения двух тел) в виде качения вокруг друг друга полевых сфер положение не имеет значения, поскольку здесь происходит поворот «пи» лишь осей гироскопов, как замены одной оси (причём с её определённым наклоном) на другую ось. Это и изображено на рисунке справа.

Необходимо различать, что центр взаимно-центрического орбитального эллипса планет относится и к центру взаимно-центрического солнечно-земного вращения только к Земле, как к ключевой планете (имеющей общую орбиту с Солнцем и образующей начальное солнечно-земное вращение), и - к Венере, как к центральной планете. Потому обозначение вращения всех планет относительно общего солнечно-земного центра вращения, как относящееся лишь к нашему окружному пространству, является условным.

Ведь ещё по Копернику в мире не может быть вещественных или стабильно расположенных центров, поскольку и солнечно-земной центр вращения совершает своё собственное движение, обозначая во вращении с другими планетами (в передаче им вращения) также некий центр. Этот центр в традиционной астрономии воспринимается точкой расположения Солнца в некоей галактике «Млечного пути».

Сам же центр этой «галактики» обозначает не что иное, как солнечно-земной центр вращения. Схема гелиоцентризма в этой связи - это уже не условность, а полное не соответствие действительности.

И это необходимо различать по причине того, что исходное планетное вращение происходит в переходном полевом пространстве расслоений, т.е. – в условиях взаимного качения всё больших планетных сфер вокруг друг друга. Это означает, что, начиная уже с Марса, имеет место взаимное качение вокруг друга солнечно-земной планетной сферы (включающей в себя вращение Венеры, Меркурия и Луны) и - сферы Марса (включающей внутреннее взаимно-центрическое вращение Марса с его Астероидной сферой).

По этой причине центр употребляемого в традиционной астрономической теории марсианского эллипса, как центр выстраиваемой орбиты Марса, относится в сферическом пространстве не к солнечно-земному центру вращения (и никак не к Солнцу, как к центру), а - к центру вращения систем «Солнце-Земля» и «Марс-Астероидная сфера». В окружном же или непосредственно наблюдаемом нами пространстве центр марсианского эллипса относится к солнечно-земному центру вращения. При этом постоянство положения оси Марса относительно звёзд обеспечивается взаимным качением внутренних планетных сфер (полей) Марса, как всей системы «Марс-Астероидная сфера» и Земли, как в составе общей взаимно-центрических сферы (поля) «Солнце-Земля».

Этим, кстати, и объясняется угол наклона марсианской оси к орбитальной плоскости и период суточного вращения Марса, как схожие с земными параметрами. Гироскопическое же или внутренне постоянство положения оси Марса обеспечивается его внутренним взаимно-центрическим вращением с Астероидной сферой.


Традиционная схема гелиоцентризма размещает планеты в зависимости от их среднего расстояния от Солнца. Но обозначение вращения планет вокруг Солнца, как материального центра, не соответствует и Копернику и действительности.

Ведь планетное вращение идёт в свободном пространстве и за счёт его структуры, а – не за счёт неких жёстких связей в виде линейно направленного притяжения планет, что не только не может образовать орбитальное вращение, но и явно препятствует ему. Не различение такого явного абсурда и является следствием неверной парадигмы исходности видимого вещества (занимающего лишь около 5-и процентов от наблюдаемой вселенной).

Восприятие полевой планетной схемы вращения в сферическом пространстве (в сочетаниях планетных полевых сфер) и в окружном пространстве (относительно солнечно-земного центра вращения) возможно только в придании движения этой схеме (хотя бы умозрительного). Схема же гелиоцентризма не согласуется с действительностью из-за нарушения принципа постоянства положения осей планет и самого Солнца относительно звёзд, в связи с этим неточными оказываются и сами расстояния планет и от Солнца, и от Земли.

Исходя из этого, необходимо рассматривать две именно подвижные схемы планетного вращения: в окружном пространстве, как вращение планет относительно солнечно-земного центра по их внешним взаимно-центрическим орбитам, и в сферическом пространстве – в виде последовательных взаимно-центрических планетных сфер. При этом для больших планет относительно Солнца и Земли рассмотрение вращения относительно солнечно-земного центра уже полностью условно.

При этом в схеме окружного пространства можно рассматривать внутреннее взаимно-центрическое вращение больших планет с их ретроградными спутниками и – вращение уже этой взаимно-центрической сферы с их Астероидной сферой. В этих условиях наглядность орбитального вращения Марса, как и вращения больших планет, предстаёт в виде наблюдения так называемых спиральных «галактик», являющихся в действительности подобием и аналогом Солнечно-земной системы.

И представляют они собою фотографический след их планетных вращений. Марс в его вращении находится в сферическом пространстве (через переходное полевое пространство) всегда радиально напротив Земли и, соответственно – Солнца. При этом он совершает внутреннее взаимно-центрическое вращение с его Астероидной сферой, что и образует эксцентриситет его орбиты.



Потому противостояния Марса (его линейное расположение относительно Земли) относятся к его именно внутренней взаимно-центрической орбите, подобной лунно-земному взаимно-центрическому вращению (воспринимаемому вращением вокруг некоего «центра масс»). И такое вращение в сферическом пространстве происходит синхронно с лунно-земным и с солнечно-земным вращением.

Но в окружном пространстве, непосредственно наблюдаемом нами, один период орбитального вращения Марса соответствует примерно двум периодам солнечно-земного вращения по причине аналогично большего радиуса орбитального вращения Марса. Потому, если бы мы наблюдали орбиту Марса из далёкого космоса, она также получила бы вид двойной спирали или вид «рукавов» так называемых галактик.

Дело в том, что вследствие вращательно-поворотной структуры пространства визуально происходит расслоение внутреннего взаимно-центрического вращения Марса с Астероидной сферой (идущего синхронно с солнечно-земным вращением) или его внутренней орбиты, что, напомним, придаёт эксцентриситет его внешней орбите. При этом определяемая величина эксцентриситета Марса в силу восприятия гелиоцентризма (вращения вокруг Солнца, а не вокруг центра внешнего взаимно-центрического эллипса, как солнечно-земного центра) даёт не диаметр, а - радиус внутренней взаимно-центрической орбиты Марса, т.е. – фактически уменьшается двое.

Ведь увеличение вдвое радиуса орбитального вращения Марса в гелиоцентризме (по сравнению с действительным радиусом), наоборот, как бы складывает, или уменьшает вдвое диаметр его внутренней взаимно-центрической орбиты. Потому диаметр внутренней марсианской орбиты вдвое больше назначаемого эксцентриситета марсианской орбиты, составляя величину около 0,57 а.е., а афелий Марса от Солнца составляет не 1,67 а.е., а около 1,95 а.е.

Исходя из этого, расстояние Марса от Солнца в его орбитальном вращении увеличивается в 1,41 раза, а от Земли - в 2,5 раза, что соответствует и действительному наблюдению размеров диска Марса. В случае же гелиоцентризма расстояние Марса от Земли должно было бы увеличиваться в 5 раз! А от Солнца – лишь в 1,2 раза, что, естественно, не стыкуется с наблюдениями.

Синхронность орбитального вращения планет с солнечно-земным вращением (как бы раскручивающем общее планетное вращение) в сферическом пространстве и разные периоды орбитальных вращений в окружном пространстве (из-за разных окружных радиусов) демонстрируются не чем иным, как часовым механизмом или вращением часовых и минутных стрелок. Не случайно потому и формула, связывающая синодические и сидерические (относительно звёзд) периоды планет, исходит как раз из схемы часового вращения.

Да и сами эти периоды являются следствием переходного полевого пространства, поскольку средняя величина этих периодов (между сидерическим и синодическим периодом) для Марса как раз и составляет два года. Так вот, когда Марс начинает орбитальное вращения от положения линейного противостояния с Землёй, как наибольшего с ней сближения (перигелия), то при совершении Марсом половины оборота вокруг солнечно-земного центра или на другой стороне внешней взаимно-центрической орбиты он занимает положение наибольшего удаления или афелия.

Земля же в окружном пространстве за этот период времени завершает свой полный орбитальный поворот синхронно с Солнцем, а потому её положение оценивается, как оказавшейся уже на другой стороне орбиты относительно Марса. Но в сферическом пространстве (через переходное пространство расслоений) Земля находится всё также радиально напротив Марса, причём - в его наибольшем удалении (в различении внутренней взаимно-центрической орбиты Марса с диаметром около 0,57 а.е.).

В окружном же или в наблюдаемом нами пространстве один орбитальный или годовой период Марса соответствует примерно двум орбитальным или годовым периодам Земли. В связи с этим один земной год относительно пространства и Марса, образно говоря, «растворяется», что и означает наглядное проявление пространственно-временной энтропии и относительности счёта временной длительности.

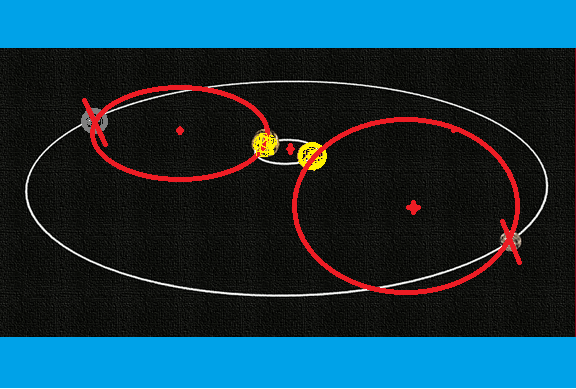
Визуально же (на примере спиральных «галактик») это выражается в том, что внешняя эллипсоидная орбита Марса относительно солнечно-земного центра вращения через марсианские полгода совершат поворот «пи» в вертикальной плоскости (при наблюдении именно спирального вида «галактик»). Это и изображено на рисунке ниже красной стрелкой и прослеживается на фотографии спиральных «галактик» (как звёздно-планетных вращений, фронтально повёрнутых к наблюдению с Земли).



Этим в полевом пространстве расслоений совмещается сферическое пространство (как пространство синхронное с однородным временем) и - окружное пространство (как пространство, обозначающее орбитальные радиусы вращения с разными периодами и с неоднородным временем). По этой причине эллипсоидная внешняя орбита Марса после совершения им половины вращения и расслаивается в спираль с образованием второй части спирали в виде рукава, чем занимает положение начальной позиции (опять перигелия с Землёй).

Это означает, что и Земля, и Солнце (обозначено жёлтым цветом) остались в той же части орбиты относительно Марса, в которой они были и раньше, но периоды их орбитальных вращений по отношению к Марсу отличаются при этом в два раза. И устраняется такое несоответствие орбитального расположения планет - их орбитальным периодам поворотом на величину «пи» пространственной структуры.

При этом левое положение относительно эллиптического или взаимно-центрического центра вращения становится правым и, наоборот. Это значит, что со срединного положения между Землёй и Марсом (с соответствующей точки Лагранжа) Марс будет достигать его афелия через земно год.

С Земли же и с Марса это время будет составлять уже два года. Потому и запуск космических аппаратов с соответствующих точек Лагранжа должен сокращать время полётов к планетам.

Подобный пространственный поворот происходит и в отношении к большим планетам. Но ввиду больших орбитальных сидерических периодов спиральность их орбит уже не так отчётлива на фотографиях звёздно-планетных вращений («галактик»)

Исходя из этого, по виду планетно-звёздных вращений («галактик» спирального, овального и иного вида в зависимости от угла наблюдения) можно сказать, что мы визуально наблюдаем сферическо-окружной пространственный переход «πи/2: πи*√2/2:πи*√2/√2» магнитной пространственной структурной и исходной частоты. Потому на этом примере такой поворот пространственной структуры на величину «пи» происходит и визуально, а не только на схеме пространственно-временной энтропии или умозрительно.

6. Пространственный структурный поворот на примере вращения Венеры.

Т.о., именно вид спиральных «галактик», являющихся в действительности звёздно-планетными вращениями, показывает и именно пространственно-структурное происхождение и планетного вращения, и – самих планет. Само же восприятие галактик, исходящее из наблюдения «Млечного пути» - окружной последовательности звёздных скоплений, является следствием наблюдения небесной сферы из солнечно-земного взаимно-центрического вращения.

Сфера Марса (как взаимно-центрическая система «Марс-Астероидная сфера») и солнечно-земная сфера образуют в два раза большую общую сферу, как системы уже «Солнце-Земля-Марс». Эта сфера, образуя соответственно свой центр вращения, совершает взаимное качение вокруг сферы Юпитера (как тройной системы «Юпитер-Спутниковая сфера - Астероидная сфера»), имеющей уже в полтора раза больший размер (чем сфера общей системы «Солнце-Земля-Марс»).

А этим образуется следующая общая сфера системы «Солнце-Земля-Марс-Юпитер», которая также получает свой центр вращения (со следующей сферой системы «Сатурн - Спутниковая сфера - Астероидная сфера»), и т.д. По этой причине центр начального солнечно-земного вращения образует спиральный след в виде яркого ядра «галактики» на космических фотографиях.

Качение таких общих планетных сфер (полей) вокруг друг друга проявляется в вытянутой орбите комет. При этом, например, комета Галлея обозначает центр вращения двух сфер, образованных до крайней сферы «Пояс Койпера» с вращением плутоноидов.

Такое вращение, имеющее отношение к заряду качения, и образует общую орбитальную плоскость планет или плоскость эклиптики за счёт проявления уже окружного пространства, как имеющего отношение к полевому заряду вращения (центростремительному ускорению). Т.о., условие постоянства положения оси вращения относительно звёзд для Земли и Луны, как и для системы «Солнце-Меркурий», обеспечивается их внутренним взаимно-центрическим вращением, но проходящем на фоне их внешнего синхронного взаимно-центрического вращения вокруг солнечно-земного центра.

В этом плане Солнце, хотя энергиозно и образует или начинает планетное вращение, но выступает в роли планеты, как рядового участника планетного вращения. Венера же, как центральная планета в солнечно-земном вращении, образует внутреннее взаимно-центрическое вращение с центральной сферой (полем) солнечно-земного вращения (как с центральной точкой Лагранжа, о чём речь дальше) с диаметром лишь около 0,042 а.е.

В связи с этим наблюдаемая орбита Венеры и получает минимальный из всех планет эксцентриситет в её вращении относительно солнечно-земного центра. О таком размере центральной сферы солнечно-земного вращения свидетельствует и перигелий кометы Галлея относительно Солнца (0,587 а.е.).

Относительно же солнечно-земного центра вращения перигелий кометы составляет 0,087 а.е., т.е., как раз примерно в два раза большей диаметра центральной взаимно-центрической сферы (также образующей взаимно-центрическое вращение и с кометой). Внешнее взаимно-центрическое вращение Венера, как центральная планета, составляет с системами «Солнце-Меркурий» (как с тройной системой, о чём речь дальше) и «Земля-Луна».

И, в отличие от орбиты Марса, получающего пространственный поворот «пи» в сферическом пространстве, орбита Венера в окружном или в непосредственно воспринимаемом нами пространстве получает вид не эллипса, а - необычный вид разомкнутой спирали. Это обстоятельство также объясняется устранением несоответствия между синхронным сферическим вращением и окружным вращением, имеющим различные периоды.

Потому в переходном полевом пространстве расслоений (в сферическо-окружном пространственном переходе) или просто в переходном пространстве, выражающем сферическое или исходное пространство, спиральная орбита Венеры (изображена зелёным цветом) смыкается в орбитальную окружность вокруг солнечно-земного взаимно-центрического центра (изображена красным цветом). И здесь также наблюдается пространственно-структурный поворот в вертикальной плоскости на величину «пи», но со сменой уже не положения (как в случае с вращением Марса), а - направления вращения.



Напомним, что вращение Марса получает в окружном пространстве несоответствие его постоянного радиального противостояния с солнечно-земным вращением (как выражения общей синхронности планетного вращения) с наблюдаемыми периодами орбитальных вращений его и солнечно-земного вращения. И устраняется такое несоответствие пространственным поворотом на величину «пи». При этом заход Марса за Солнце – это лишь кажущееся движение, схематически высчитываемое.

Также и во вращение Венеры её заход за Солнце, как следствие её соответственно меньшего орбитального периода, - это лишь воспринимаемое явление, которое, в отличие от вращения Марса устраняется, как несоответствие, смыканием спирали в орбитальный эллипс внутреннего взаимно-центрического вращения в виде также пространственно-структурного поворота на величину «пи».

В связи с этим космос мы наблюдаем двойственно – в сферическом пространстве (через воспринимаемое нами переходное пространство) и – в окружном пространстве. Марс, не заходит за Солнце, поскольку вращается качением в составе своей взаимно-центрической сферы относительно общей солнечно-земной сферы, образуя с Солнцем и Землёю лишь противостояние (постоянное радиальное и периодическое, через два года - линейное). А этот факт чрезвычайно важен для космических полётов на Марс.

Венера также не заходит за Солнце, имея сферическое (происходящее в сферическом пространстве) вращение вокруг солнечно-земного центра. Потому можно сказать, что соединение и всех планет (кроме Меркурия) с Солнцем – это, как и их попятное движение, лишь видимый или наблюдаемый эффект в силу именно сферическо-окружного пространственного перехода. И действительно, расположение Марса, Венеры и больших планет за Солнцем относительно Земли означало бы вращение и их, и Земли вокруг Солнца.

Но вращение вокруг Солнца противоречит принципу постоянства положения осей вращения планет и оси самого Солнца относительно звёзд. Орбитальный эллипс же больших планет вообще относится к их внутреннему взаимно-центрическому вращению со сферой ретроградных планет (что образует и наблюдаемый их синодический период).

При этом внешнее взаимно-центрическое вращение больших планет, что сохраняет положение их осей относительно звёзд, относится уже к вращению с их астероидными сферами в составе их общих взаимно-центрических сфер. И период такого вращения относится к непосредственно не наблюдаемому сидерическому периоду орбитального вращения больших планет.

Сферическо-окружной пространственный переход, оказывается, визуально наблюдаем и в непосредственном солнечно-земном вращении, причём - также на примере наблюдения Венеры. Дело в том, что расстояние Венеры и от Солнца, и от Земли вследствие её орбитального вращения вокруг солнечно-земного центра изменяется примерно в 2,57 раза (как отношение 0,72 а.е./0,28 а.е.).

Но поскольку радиус сферического вращения (4пиR) в два раза меньше радиуса окружного вращения (2пиR), а эллипс орбиты Венеры относится как раз к сферическому вращению, то наблюдаемый с Земли диск Венеры визуально изменяется уже более чем в 5 раз, что и соответствует наблюдениям.

При этом и перигелий Венеры относительно Солнца уменьшается в сферическом пространстве в два раза (становясь величиной в 0,14 а.е.). Кстати, восприятие гелиоцентризма и среднее расстояние Меркурия от Солнца увеличивает в два раза, поскольку вращение планет фиксируется в действительности идущим вокруг солнечно-земного центра, а назначается вокруг Солнца, чем и диаметр орбиты планет назначается их радиусом, т.е. – увеличивается в два раза.

Схема же гелиоцентризма и вращение Меркурия рассматривает идущим вокруг солнечно-земного центра (не зная об этом), увеличивая этим в два раза и диаметр его орбиты, и чем объясняется большой эксцентриситет Меркурия. В связи с этим расстояние Меркурия от Солнца необходимо оценивать величиной примерно в 0,195 а.е. (в окружном пространстве).