1.Триальная пространственно-временная энтропия или инверсия пространственных объёмов.

В сферическом или в исходном (вакуумном) пространстве, поскольку нет понятия размерности, то нет и окружных плоскостей, ограничиваемых радиусом. Начальный же в отношении к нашему пространству радианный поворот «пи/2», как расслоение исходной взаимно-центрической структуры на частотную и контурную составляющую или образующую, оформляет и поворотное вращение, как четверть полной или контурной окружности (её длины) – «πR/2», чем возникает центр вращения, а значит – и радиус.

Относительно же нашего окружного пространства полевая окружность образуется поворотом на радианную величину «пи» полуокружности «пи», образованной в переходном пространстве расслоений. Полуокружность формируется при этом срединным пространственным объёмным поворотом «πи/√2», как наложением исходного взаимно-центрического вращения на окружное стягивание поворотности нашей пространственной среды, что можно обозначить контурным или силовым следом такого наложения.

А за счёт возвратности или цикличности сферическо-окружного перехода магнитной исходной частоты «πи/2:πи/√2:πи» он принимает вид «πи:πи/√2:πи/2». И в связи с этим в отношении к исходному сферическому пространству, наоборот, полные окружности (называемые круговыми слоями) относятся к этому пространству, образуясь за счёт объёмной или сферичной спиральности звена «πи/√2» в общем пространственном переходе. И расслаиваются такие слои до радианного поворота «пи/2» в поле силы тяжести, как уже в массовом пространстве (см. параграф №5 Введения). Это значит, что первое переходит во второе и наоборот, второе – в первое, но с различением источника такого перехода – сферического пространства и сферического или поворотно-вращательного объёма и с различением уже невозвратности окружного или статичного объёма нашего пространства.

Кроме того, поскольку в начальном сферическом или в кинематическом пространстве нет размерностей, то и возможность оценки нами объёма (в виде подвижного сферического объёма, измеряемого частотой поворотных пульсаций) появляется лишь в начальном переходном пространстве. В связи с этим и сферическо-окружной пространственный переход структурно относится к переходному полевому пространству расслоений с оформлением вначале безразмерного сферического объёма (Vs1=T2) в виде квадрата длительности, как инверсионной величины по отношению к частоте, оформляемого за счёт объёмной спиральности перехода «πи/√2». И завершается общий переход «πи/2:πи/√2:πи» невозвратным (для молекулярных образований) окружным объёмом нашего состояния пространства (для сферы это выражение «Vr= 4/3пиR3»). Размерный же сферический объём также в размерности квадрата длительности (что есть взаимно-центрическим сопряжением), но выражаемый уже через радиус, образуется во второй части переходного пространства или в предмассовом пространстве (Vs2=T2=4пиR/g0).

В этой части пространства формируются взаимно-центрические планетные сферы. Окружной стационарный объём видимых или наблюдаемых нами планет (в размерности третьей степени длины) – это уже массовое пространство. Начальное переходное пространство с «чисто» сферическим или поворотным объёмом можно назвать и гиперпространством, размерный же сферический объём ранее обозначен в теории различения (4) срединным вакуумным пространством, а полевое пространство окружного объёма или массового пространства было названо наружным вакуумным «слоем» пространства.

В рассмотрении упомянутых трёх видов объёмов происходит и трёхкратный сферическо-окружной переход магнитной структурной частоты, что говорит о трёхсложности и самого структурного сферическо-окружного перехода, как трёхсложной и трёхсоставной или триальной пространственно-временной энтропии (3, стр. 242). Такой общий кинематико-динамический переход или инверсия, обозначаемая в виде rot (rot (rot)) как «вращение вращения во вращении» и состоящая каждая из перехода «πи/2:πи/√2:πи» магнитной структурной частоты, и приводит к образованию статичного или динамического окружного объёма нашего пространства (для сферы это выражение «Vr= 4/3пиR3»).

Постоянная же цикличность такого перехода, как бы отражающего самого себя или как зеркальная запись перехода «πи/2:πи/√2:πи»/«πи:πи/√2:πи/2», означает образование 3-х поворотной структуры сферического объёма и 4-х поворотной структуры полевого объёма окружного. Эти пространственные объёмы переходят друг в друга, но образуя выделение в массовом пространстве из 4-х поворотного окружного объёма - полностью стянутого и невозвратного молекулярного объёма (в виде видимых тел, внешне отделённых от пространства). В связи с этим и вид окружного объёма для сферы «Vr= 4/3пиR3» можно представить четырьмя окружными полевыми поворотами «пи/2» в отношении их к трём перпендикулярным сферическим таким же поворотам «пи/2», и всё это – через операцию отражения «пи». Образование же при этом окружного объёма уже и через трёхкратное сопряжение радиуса означает молекулярный окружный объём, как выделение видимого вещества из общего невидимого или полевого пространства-вещества переходного пространства.



Таким образом, речь необходимо вести не о мерности пространства (что есть абсурд, поскольку пространство-время и образует вещество и его меру), а – о поворотной триальной энтропии пространства-времени (причём в действительном понимании энтропии, как исходного пространственного преобразования). При этом пространство-время необходимо воспринимать не абстрактными событийными координатами на некоей аморфной сцене материальных процессов, а – нераздельными, но вместе с тем и не слитными понятиями. Это и есть обозначенное ещё Ньютоном (и продолженное А.Эйнштейном через придание пространству-времени физических атрибутов, как в первую очередь метрики и кривизны, которые и влияют на процессы, и сами зависят от них) - вмещение или образование пространством и временем самих себя.

Кроме того, в указанном трёхсложном и 3-х составном или триальном переходе магнитная частота «106» из не воспринимаемой нами исходной частоты поворотных пульсаций становится сначала фоновой частотой фоновых (электромагнитных) волн. Затем эта преобразованная за счёт объёмной инверсии частота становится косвенно нами воспринимаемой (например, в магнитном ядерном моменте) ядерной частотой. А после того она становится и явно воспринимаемой молекулярной частотой магнитного взаимодействия в виде интенсивности магнитного взаимодействия (но в также размерности частоты) «106».

Взаимно-центрическое же сопряжение уже магнитной частоты в такой же последовательности образует и чувственно воспринимаемую нами электрическую структурную частоту «1012», становящуюся затем контурной оболочковой молекулярной частотой 5,85*1011. Можно сказать, что приведённый постоянно идущий триальный энтропийный пространственно-временной процесс и создаёт весь набор частот для фоновых или электромагнитных волн, что проявляется в фоновом космическом излучении. А это значит, что и гравитация, и фоновые или электромагнитные волны – это проявление одного и того же процесса – триальной пространственно-временной энтропии. Ещё одно подтверждение единства вселенной У.Рассела.

2. Сущность срединного пространственного перехода «πи/√2», как пространственно-временной зазор

Т.о., в своей цикличности сферическо-окружной переход «πи/2: πи/√2: πи», составляя и всю объёмную пространственно-временную энтропию, согласно частотно-контурному строению вещества (3) является не только трёхсложным, но – и трёхсоставным, что означает и трёхкратный поворот «пи» или радианный поворот на 180° гравитационной пространственной структуры. При этом образуются полевые квадруполи или четырехсферники, а вместе с ними через триполи или трехсферники, как через промежуточные образования, – и септуполи или семисферники и далее - сложносоставные уже молекулярные образования.

Доказывается такое обстоятельство математическим выражением постоянной электрической величины, что одновременно есть и структурным обозначением электрона, как «8,85*10‾¹²≈((4*7π)/10)* 10‾¹²» (4, стр. 152). Это значит, что число «пи» является не только радианным выражением величины или угла поворота, но и математически оформляет постоянные величины, как иррациональное число «пи» (величиной 3,14159…).

Числитель постоянной величины Зоммерфельда, обозначающий срединное звено перехода магнитной частоты «πи/√2», в триальной пространственно-временной энтропии относится не только к также срединному частотно-контурному или квантовому переходу в предмассовом пространстве, проявляемому в световом спектре тонких ядерных структур. Он входит в состав и двух других подобных переходов «πи/2: πи/√2: πи» магнитной структурной частоты при её фоновом пространственном преобразовании. При этом начальный переход «πи/2» (как начальное звено в гиперпространстве или в пространстве начального сферического объёма и как начальное звено в двух других видах пространственного объёма) структурно проявляется в перпендикулярности друг другу магнитной и электрической напряжённости фоновых (электромагнитных) волн.

А вот конечный переход в виде поворота «пи» - это и явно наблюдаемый эффект отражения. Числитель постоянной величины Зоммерфельда «πи/√2*106» (обозначенный Н. Козыревым скоростью перехода причины в её следствие) потому и регистрируется в виде постоянной величины, что обозначает некий структурный «доворот» (дополнительный «стянутый» спиральный поворот) в проявлении пространственной структуры, формирующей и «чистую» сферическую объёмность, и размерную объёмность (сферическую и окружную), и частоту фоновых (электромагнитных) волн, и длительность ядерных и молекулярных взаимодействий.

При этом срединный пространственный переход «πи/√2» исходной магнитной структурной частоты равен, кроме того, и максимальной интенсивности взаимно-центрического взаимодействия двух электритов, как максимально скрученных в их сопряжёнии минимальных электрических сфер или электронов (называемых минимальными зарядами): (πи/√2)*106=е2/4пи * (3, стр. 79). Это значит, что объёмный или спирально-сферический поворот «πи/√2» (как «доворот» в среднем на 45° в перпендикулярной плоскости к начальному повороту расслоения «пи/2») происходит вследствие образования минимального радиуса взаимодействия двух электритов «е» в виде √ (как корня квадратного из редуцированной постоянной величины Планка). Здесь необходимо упомянуть, что электрит – это ещё не «готовый» электрон в его скрученном или сопряжённом состоянии (от размера вращения электрона «4*10ˉ10 м.»), а – гипотетический первичный частотно-контурный бозон (3,стр. 117).

И обратим внимание, что величина (корень квадратный из редуцированной постоянной величины Планка) √ (равная 1,0266*10ˉ17 «м») значительно больше сопряжённого размера вращения электрита (16*10-20 «м»). А это значит, что электриты образуют между собой пространственно-временной зазор величиной, равной примерно среднему радиусу сопряжения электритов (0,342*10ˉ17«м»), как третьей части величины √ , что изображено на рисунке ниже. Причиной этому и есть «доворот» в перпендикулярной плоскости, образующий, кроме того, и пространственную временную задержку (обозначенную Н.А.Козыревым скоростью перехода причины в её следствие), и проявляющий не симметричность нашего окружного или динамического пространства. Вследствие этого электриты (до образования невозвратного окружного объёма) ещё не образуют восьмеричного или дипольного образования ядерно-молекулярного стягивания, а следуют взаимно-центрическому (но уже размерному) спиральному и вместе с тем сферическому вращению скручивания и раскручивания (за счёт того же «доворота»).

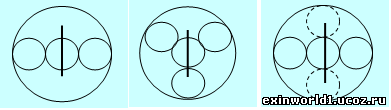
Центральный электрит при этом перпендикулярно развёрнут в окружном восприятии относительно двух других электритов (что обозначено вертикальной линией), вследствие чего они и воспринимаются некими волокнами (3, стр.120). Частотно-контурный, сферическо-окружной или кинематико-динамический пространственный переход – это возвратный цикличный процесс (но с оформлением невозвратного окружного молекулярного объёма). Потому факт «пространственно-временного зазора» между электритами, равный и их усредненному размеру вращения означает, кроме того, и само их образование операцией двухстороннего отражения «пи», как звена в переходе «πи/2: πи/√2: πи» магнитной структурной частоты.

Поскольку величина «√ »(корень квадратный из редуцированной постоянной величины Планка), действительно, не может быть неким «волшебным» размером, препятствующим сближению электритов и ядерных нуклонов, то она может означать только одно: начало с этого расстояния процесса отражения двух электритов с образованием центрального третьего электрита. Этим и проявляется исходный пространственный триполь или трёхсферник, что изображено на рисунке вверху слева.

Тройное же отражение центрального электрита, называемого в теории Е8 «кругом электромагнетизма» (3, стр. 120), в обратном процессе расслоения образует уже 3-х аксиальную структуру четырёхсферника или квадруполя, как, например, магнитный квадруполь в структуре электрона (3 стр.51) (он показан на рисунке верху в середине). В четвёртой же операции отражения образуется уже структура пятисферника (на рисунке вверху справа), например, воспринимаемого пятигранником на схеме Зоммерфельда для электрического поля вокруг ядра (3 стр.53).

Т.о., срединное звено сферическо-окружного перехода магнитной структурной частоты «πи/√2» в трёх составных объёмных инверсиях общего сферическо-окружного перехода можно представить и в трёх видах взаимодействий электритов, переходящих во взаимно-центрическое вращение гравитонов. При этом указанные три вида пространственных переходных взаимодействий обозначают и три вида пространственных полевых объёмов, как фазы пространственного перехода. На рисунке вверху слева – это сферический поворотный объём, относящийся к электронам и к частицам с половинчатым спином (фермионам), а в космическом пространстве – к гиперпространству и к внутренним симметричным взаимно-центрическим полям или сферам. В середине – это сферический размерный объём, относящийся к ядерной структуре и к предмассовому пространству, а в космическом пространстве – к взаимно-центрическим планетным сферам или полям, образуемым взаимно-центрическим вращением гравитонов. Справа же – это уже массовое полевое пространство и полевой (контурно не стабильный) окружной объём, что в космическом пространстве – это поле планетного вращения.

И все эти преобразования относятся и к числителю постоянной Зоммерфельда и к скорости перехода причины в её следствие Н.Козырева, как к проявлению из непрерывного симметричного и сферического пространства нашего дискретного и асимметричного окружного пространства. В дальнейшей же операции пространственного отражения образуется уже невозвратный молекулярный объём. Такая структура пространственного перехода показывает, что пространство-время образует самое себя. Ведь срединное звено пространственного перехода «πи/√2», будучи в радианном (временном) выражении объёмным (спирально-сферическим, как проявляющим полевое скручивание и раскручивание) «пространственным доворотом», в числовом выражении обозначает фазность пространства в том, или ином графическом виде пространственного объёма.

3. Ракетное движение и частотное преобразование фазового перехода пространственного тяготения.

Пространственный структурный «доворот» «πи/√2» в форме четырехсферника или в фазе срединного сферического размерного объёма – это уже не три электрита или триполь, а гравитон, который в операции отражения «пи» образует спиральное взаимно-центрическое вращение в проявлении полевых пространственных сфер. Гравитон выражается его размером вращения, как 4пиR=3.47*10‾17 «м» (4, стр. 126), исходя из формулы оборотного маятника через световую длительность (как через обратную величину частоты распространения света в нашем пространстве).

В связи с этим, действительно, можно утверждать, что видимое вещество образуется электромагнетизмом и проявляется светом, как и писал У.Рассел. При этом, поскольку пространственный полевой переход – это процесс цикличный, то гравитоны, хотя и начинают оформлять размерный сферический объём, но объёмно (в объёмном размере) или графически их невозможно выделить из пространства в отличие даже от фотонов, как первичный бозонов (3, стр.142).

Дело в том, что расстояние между центрами двух начальных гравитонов (0,2236*10‾17 «м»), образующих взаимно-центрическое вращение, - это линейное выражение объёмного структурного «доворота» «πи/√2». В связи с этим можно оперировать лишь квадрупольным размером вращения гравитона «4пиR», соответствующим и размеру нуклона в ядре.

Срединное звено «πи/√2» частотно-контурного пространственного перехода «πи/2:πи/√2:πи» магнитной структурной частоты проявляется не его следствием (как, например, при приведённом различении схемы морских приловов и отливов), а – и наглядно далеко не только в эффекте Джанибекова. Оказывается, это различение и ракетного движения, броска бумеранга и даже механики полёта птиц и насекомых, или машущего полёта. При этом ракетное движение ярко проявляет кроме пространственного сферическо-окружного перехода и частотно-контурное выражение наружной силы согласно физике различения (4, стр.82), как произведение силы внутренней (в размерности «кг») на импульс силы (в размерности 1/сек²).

Ведь ракета движется и в космосе или в безвоздушном пространстве, т.е. – без наличия среды отталкивания, как второго взаимодействующего тела в употребляемой физической теории. В связи с этим и бытующее объяснение такого движения подобием выстрела из пушки не уместно, поскольку ракета - это не снаряд и движется в свободном пространстве (без всяких вторых тел), а не в дуле орудия, за счёт тела которого пороховой заряд своим взрывом образует направленное силовое импульсное воздействие на снаряд. Взрыв порохового заряда в замкнутом вытянутом пространстве с одним выходом увлекает таким выходом порохового газа и снаряд.

Но за счёт чего движется ракета при выхлопе горящего топлива из её двигателя? Здесь уже нет замкнутого пространства для образования толчка, а в космосе нет даже и воздуха, а потому согласно употребляемой пока теории, в которой пространство - это лишь вещественная пустота, никак не воздействующая на тело, ракетные выхлопы должны были бы так и уходить в пустоту без всякого воздействия на ракету.

Удивительно, что теоретики до сих пор не различают данный факт. И это можно объяснить только тем, что они боятся даже затрагивать вопрос о пространственной полевой структуре, как о категории, которая полностью подрывает все устои пока употребляемой физической теории. И за счёт чего движется ракета в открытом космосе, от чего она отталкивается там, где существует почти полный вакуум? Естественно, - только за счёт проявления поворотно-вращательной структуры пространства. Данное свойство пространственной структуры явно проявляет не только упомянутый выше эффект Джанибекова, симметричные лунные приливы, но и опыты с диском и стержнем, подвешенным на нитке к ротору электродвигателя (18).

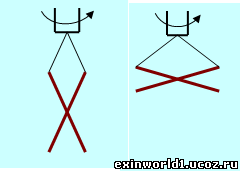
При наблюдении опыта видно (изображён на рисунке ниже), что вращение стержня или диска, подвешенного на нитке к валу электромотора, за счёт гибкости нити не становится вращением вокруг его оси, повторяя вращение ротора. Вращение нити образует конус, повторяя рисунок пространственного конуса фазового структурного перехода «πи/2:πи/√2:πи» магнитной исходной частоты такого перехода. И напомним, что переходное (к нашему окружному пространству) пространство расслоений различается на предмассовое или чисто полевое и массовое пространство, где проявляются уже молекулярные формы и силовые поля или сферы.


Так вот фазовый структурный переход пространственного тяготения с магнитной исходной частотой, относясь к исходному или сферическому пространству, образует предмассовое пространство, индуцируя или возбуждая световое излучение. Световое же излучение, повторяя исходную структуру фазового пространственного перехода «πи/2:πи/√2:πи» проявляет и непосредственно наше (воспринимаемое нами) массовое пространство в виде уже диапазонов фоновых или электромагнитных волн, т.е. - весь соответствующий набор частот структуры фазового перехода. Ведь универсальность тяготения предполагает и универсальность частоты фазового перехода в тяготении пространства.

Именно такое явление частотного преобразования фазового пространственного перехода, как преобразование предмассового пространства в массовое пространство, и обозначил У.Рассел, говоря о том, что всё видимое вещество образовал свет. В связи с этим частота распространения света в том или ином массовом пространстве становится частотой распространения и всех фоновых (электромагнитных) волн, получающих диапазонный набор собственных частот или частот излучения. Потому при фазовом цикличном или возвратном полевом переходе «πи/2:πи/√2:πи»/«πи:πи/√2:πи/2» в массовом пространстве действует в первую очередь сама структура перехода, а не его частота.

Исходя из этого, числитель постоянной величины Зоммерфельда, как и скорость перехода причины в её следствие Н.Козырева, относясь к световым явлениям и к атомному ядру в числовом виде, в виде структурном относятся уже ко всем наблюдаемым явлениям и частотам нашего окружного пространства. Исходя из этого, и обозначается структурная универсальность фазового структурного полевого перехода.

4. Проявление пространственного полевого перехода в ракетном движении.

Срединное звено «πи/√2» доворота (радианный поворот "пи", делённый на корень из двух) и означает угол пространственного конуса величиной около 37°30' к начальной или вертикальной оси вращения. Не случайно именно под этим углом и производиться метание спортивного копья или диска. При этом в объёмном виде конус образует, естественно, окружной диполь, что выражается во вращении стержня вокруг его точки симметрии с образованием уже восьмеричного вращения. Восьмеричное же вращение или то, что конусное вращение, вызываемое воздействием пространственной структуры (её фазовым переходом), симметрично раздваивается, а не образует лишь один конус, свидетельствует о неизменном взаимно-центрическом характере такого пространственного полевого вращения.

При этом стержень через половину окружного поворота «2пи» или через радианный поворот "пи" видимым образом (или в предмассовом полевом пространстве) начинает уже изменять и направление своего вращения, что соответствует записи пространственного фазового перехода «πи/2:πи/√2:πи». Изменение направления вращения и напоминает эффект Джанибекова, и подчёркивает полевое образование окружного вращения "2пи" или вращения на 360 градусов в нашей пространственной фазе через операцию отражения (как перпендикулярного поворота «пи») радианного окружного поворота "пи" (поворота на 180 градусов или на полуокружность) в переходном и предмассовом пространстве. И при увеличении частоты вращения стержня или диска (преодолевающей силу тяжести), вследствие чего может расширяться угол вращения нитки, проявляется уже и перпендикулярный пространственный радианный поворот «пи/2» в виде смены начальной вертикальной оси вращения на перпендикулярную к ней или на горизонтальную ось. После этого стержень или диск начинает вращаться уже в горизонтальной плоскости (см. рисунок вверху справа). А то, что структурные пространственные конуса не исходят из одной точки, является следствием проявления фазового перехода, как временной задержки, и одного из принципов взаимо-центризма или того, что в открытом пространстве нет вещественных центров (о чём писал ещё Н.Коперник).

Фазовый пространственный переход, как непрерывный и возвратный или зеркальный «πи/2:πи/√2:πи»/«πи:πи/√2:πи/2» (отражающий сам себя), подтверждается, кроме того, и эффектом поляризации двух фотонов (разделённых из одного) всегда по перпендикулярным друг к другу осям. При этом так называемую "поляризацию" необходимо понимать лишением фотона сферического или «4пи» вращения с оставлением лишь окружного пространственно-полевого вращения «2пи».

Приведённое поведение вращающегося диска или стержня, подвешенного на нити, в отсутствии каких-либо регистрируемых полей может быть только следствием проявления полевой пространственной структуры поворотно-вращательного свойства, а именно – в виде фазового структурного перехода с магнитной исходной или начальной частотой этого перехода, становящейся в частотном преобразовании частотой вращения стержня. Из этого опыта можно сделать вывод, что пространственный объёмный симметричный или восьмеричный конус вследствие возвратности или цикличности фазового структурного перехода (в виде его зеркальной записи «πи/2:πи/√2:πи»/«πи:πи/√2:πи/2») всегда сопровождается образованием перпендикулярного к нему другого объёмного конуса. Ведь сама объёмность пространства, как наличие сферы вращения стержня, уже предполагает образование двух перпендикулярных конусов, как структурных проявлений «доворота» «πи/√2» или срединного звена в фазовом переходе. При этом один из конусов находится в массовом пространстве (обозначая видимое конусное вращение), а другой в – предмассовом или в «чисто» полевом пространстве, но с возможностью перехода друг в друга (также из-за цикличности фазового перехода).

При вращении диска или стержня на нитке пространственный конус проявляется резонансом на частоту вращения диска или стержня. А в обратном порядке и при выхлопе газов из сопла ракетного двигателя такой резонанс от пространственного конуса заставляет и газовый выхлоп ракеты также принять форму конуса (на рисунке ниже изображён оранжевым цветом), причём с таким же радианным углом доворота «πи/√2» или примерно под 37 градусов к оси сопла. Ведь дело в том, выхлопы из-за округлой формы сопла выходят в состоянии вращения, чем и уподобляются стержню, подвешенному на нитке. Потому и чем больше вращение выхлопов или их частота, тем и эффективнее движение ракеты (турбореактивные двигатели).


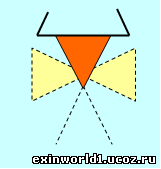
Но также подобным образом здесь проявляется и перпендикулярный пространственный восьмеричный конус (изображён на рисунке жёлтым цветом), который и служит как бы постоянно образующейся опорой для отталкивания ракетных газовых выхлопов. Потому и можно сказать, что ракетный выхлоп отталкивается как бы от самого себя. При этом отталкивается, естественно, не сам молекулярный ракетный выхлоп, а его полевое наполнение, которое и заставляет оформляться выхлопу в конус. А оформление выхлопа в конус делает внутреннюю или полевую силу отталкивания уже явной или наружной силой ракетной тяги.

При движении же ракеты за счёт возникшего таким образом силового импульса вдобавок образуется и силовая инерционная цепочка в виде таких же двух перпендикулярных дипольных объёмных конусов, как трёх силовых пространственных сфер. И от них также отталкивается ракетный выхлоп. В связи с этим и можно сказать, что ракетное движение даже не вдвое, а втрое эффективнее обычного движения.

5. Пространственный полевой переход в полёте бумеранга.

Доворот «πи/√2» магнитной исходной частоты образует и общее спиральное взаимно-центрическое полевое движение, становящимся взаимно-центрическим звёздно-планетным вращением. Ведь постоянная цикличность фазового перехода тяготения пространства (его запись, как «πи/2:πи/√2:πи»/«πи:πи/√2:πи/2») до пределов молекулярного состояния и означает формирование полевой пространственной структуры именно срединным звеном структурного доворота «πи/√2» магнитной исходной частоты «106» и затем частоты образованного вращения. И проявляется такое полевое свойство пространственного тяготения (с учётом частотного преобразования фазового пространственного перехода) наиболее ярко в полёте возвратного бумеранга. Бумеранг, напоминая своей конструкцией двухлопастной и четырёх лопастной (в форме креста) пропеллер, при его свободном вращении после броска образует, как и гайка Джанибекова, переходное состояние между открытой и закрытой системой вращения (см. параграф 2.15).

Дело в том, что, например, сплошной диск или колесо образуют закрытую систему вращения, поскольку частотная наружная спиральная образующая равна контурной спиральной образующей, а этим равны контурные и частотные сферические радиусы вращения. Такое обстоятельство, кстати, и не даёт вращающемуся колесу упасть в процессе его свободного качения. Но разделённый на лопасти диск, причём через радианную величину «πи/2» или через 90 градусов уже не формирует в его вращении закрытую систему вращения. Ведь сфера вращения такого диска в виде бумеранга в предмассовом и массовом переходном пространстве этим разрывается, становясь подвержённой тяготению исходного сферического пространства, а значит, и – сферическо-окружному переходу «πи/2:πи/√2:πи». Расположение лопастей под 90 градусов друг к другу делает частотный радиус переменным через его спиральное формирование, чем и не выполняется условие равенства частотного и контурного радиуса полевой сферы вращения для совершения устойчивого инерционного вращения.

Запущенный в вертикальной плоскости бумеранг примерно через 2/3 его оборота отклоняется влево и одновременно поворачивается вправо примерно на радианную величину «пи/2». 2/3 же оборота - это как раз и есть примерное соответствие числового или полного содержания срединного звена перехода или доворота «πи/√2», выраженного в градусах. Это и означает, что при запуске возвратный бумеранг сразу же подпадает под воздействие сферическо-окружного перехода магнитной исходной частоты или под воздействие пространственного тяготения. Здесь, как и в случае ракетного движения, также можно сказать, что инерционная силовая сфера или силовое поле запущенного бумеранга вследствие вращения сферы, а значит, - и вращения бумеранга, резонирует с полевой структурой пространственного тяготения, которая как бы отражается на инерционном поведении бумеранга.



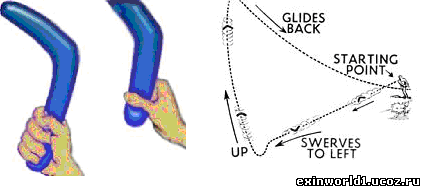
Поворот же бумеранга на радианную величину «пи/2» за счёт доворота «πи/√2» приводит, как и в случае с гайкой Джанибекова, к повороту бумеранга на радианную величину «пи» относительно оси вращения, чем и изменяется направление его вращения, а значит, - и направление его общего инерционного движения. Причём поворот «пи», проявляясь в инерционном движении бумеранга, является здесь следствием срединного доворота «πи/√2», как спирального вращения пространственного полевого тяготения, поскольку, если бумеранг не ловить, то он совершает спиральные вращения с всё меньшим или с всё затухающим радиусом вращения. И проявляется такая полевая спиральность пространственного тяготения в резком уходе бумеранга влево вместе с его подъёмом вверх (задирается вверх передняя часть плоскости круга вращения), что и изображено на рисунке вверху справа.

Такой поворот вращающегося бумеранга в его инерционном движении на радианную величину «пи» или на 180 градусов, внешне похожий на поворот гайки Джанибекова, но с направлением движения вверх, - это следствие воздействия на него инерционной силовой цепочки, как именно метания бумеранга. Иными словами, метание бумеранга придаёт ему импульс линейного горизонтального движения, а силовая инерционная сфера или поле, сохраняя или повторяя приданный импульс, заставляет вместе с тем бумеранг вращаться.

Вращение же бумеранга из-за его конструкции приводит к воздействию на него фазового структурного или полевого перехода тяготения пространства, вследствие чего импульс линейного движения становится направленным вверх или вертикально, причём с поворотом на 180 градусов от начального положения. В связи с этим изогнутый под 90 градусов конец бумеранга и способен, например, поразить дичь, на которую велась охота. Вот как описывают бросок бумеранга аборигенами Океании очевидцы: «Охотник-абориген увидел, что в его сторону на небольшой высоте летит стая птиц. Охотник невысоко метнул бумеранг на уровне плеч параллельно земле в направлении стаи. В момент, когда бумеранг оказался под стаей, он вдруг взметнулся вверх, ворвался в стаю и убил несколько птиц, чем разогнал всю стаю. Затем снаряд развернулся влево и, снижаясь, возвратился прямо в руки аборигена».

Продолжающееся инерционного вращение бумеранга прерывает его движение вверх, принуждая его к спиральному движению, а значит – и к возврату примерно в точку броска. То, что поведение запущенного бумеранга объясняется полевой структурой пространственного тяготения поворотно-вращательного свойства, а не аэродинамическими и гироскопическими эффектами (что пытаются «объяснить» без знакомства с тяготением пространства), доказывается независимость его поведения от скорости или импульса запуска.

Если бумеранг запустить, например, с вдвое большей скоростью, то и скорость наклона его плоскости (и дальнейший поворот на 180 градусов) также увеличится вдвое. И в результате бумеранг опишет почти такую же спиральную кривую. Потому диаметр этой кривой не зависит ни от скорости вращения бумеранга, ни от приданного ему начального импульса, чем длина пути определённой модели — величина почти постоянная. Также и факт необходимости запуска бумеранга строго в вертикальной плоскости (без его горизонтального заваливания) может только следствием воздействия на него полевой структуры тяготения пространства.

При запуске бумеранга в горизонтальной плоскости (как летающей тарелочки) вместо подобной спирали траектории или траектории возвращения он вначале уйдёт в небо, а затем катастрофически устремится вниз. Начальный радианный поворот «пи/2» в фазовом переходе «πи/2:πи/√2:πи», отражаемый на поведении бумеранга, и означает поворот его в вертикальную плоскость и перенос этим инерционного импульса броска вверх. Последующий же поворот «пи» или на 180 градусов через срединный структурный «доворот» «πи/√2» приводит к воздействию на бумеранг поля силы тяжести (как силы падения), прерывая его спиральное движение, вследствие чего бумеранг и устремляется вниз.

6. О механике машущего полёта птиц и насекомых или от чего они отталкиваются в полёте.

Ракетное движение в рамках употребляемой пока физической теории пытаются «объяснить» наличием в природе противодействия на любое действие, не затрагивая при этом сам механизм возникновения противодействия даже в вакуумной среде, чем фактически не затрагивают и само объяснение. Полёт бумеранга пытаются представить аэродинамическими эффектами (хотя бумеранг подобно движется и в вакууме). А вот машущий полёт насекомых и птиц уже предстает однозначной загадкой для употребляемой физической теории, поскольку механизм машущего полёта уже никак не может быть объяснён взаимодействием тел, явно демонстрируя полевую структуру тяготения пространства.

Например, давно установлено, что (19, стр.41) согласно законам применяемой аэродинамики майский жук не может летать, хотя он, как известно, вполне сносно летает. Получается, что майскому жуку не нужна подъёмная сила от контакта крыльев с воздухом. При наблюдении за птицами можно заметить, что они, подпрыгнув, машут крыльями с первого взгляда в вертикальной плоскости, но при этом не движутся вверх, как можно было бы ожидать, а сразу начинают лететь вперёд. Потому и здесь контакт крыльев с воздухом играет второстепенную роль.

То, что насекомые и птицы, оказывается, не отталкиваются от воздуха, а используют его лишь для парения, свидетельствую и такие факты, что, например, чёрный стриж, умещающийся в кулаке, с маленькими крыльями, не снабжёнными грудными мышцами, может показывать скорость полёта порядка 150 км/час, причём проводя почти всю свою жизнь в полёте. Также и бурокрылая ржанка с размахом крыльев всего в 34 см. с таким же отсутствием грудных мышц летит от Алеутских до Гавайских островов, т.е. 3 300 км без всякой посадки со средней скоростью в 90 км/час!

Но и снабжённые мышцами птицы используют их совсем не для отталкивания от воздуха, а для интенсивности взмахов их крыльев. Например, сокол в стремительном полёте несет добычу, в 5 раз тяжелее, чем он сам, на что не способен ни один самолёт. А степной орёл может совершать манёвры пикирования к земле со сложенными крыльями и, не долетая до неё лишь несколько сантиметров, выгибает шею головой вверх и лишь простыми взмахами крыльев не только останавливает стремительное падение своей большой массы, но и взмывает вверх в небо туда же, откуда и падал.

В примере с орлом уже вполне понятно, что подъёмная сила, преодолевающая и силу его падения, возникает никак не за счёт взаимодействия крыльев с воздухом или отталкивания от него. Потому и исследователи, изучавшие механику полёта птиц и насекомых, хотя и не решаются озвучить отсутствие отталкивания их крыльев от воздуха, но пишут (19,20), что «основное назначение крыла насекомого заключается не в создании подъёмной силы за счёт взаимодействия с потоком воздуха, а – в обеспечении высокой скорости крыла». Причём эта скорость, как угловая частота взмахов крыльев, всегда наблюдается наряду с устойчивой их циркуляцией и относительно продольной оси, как перпендикулярной к «чистым» или поперечным взмахам. Такое сопряжение и приводит к возникновению подъёмной силы и силы тяги.

Так от чего же отталкиваются и птицы, и насекомые в полёте? Ясно, что сопряжение чистых или вертикальных взмахов с перпендикулярной к ним циркуляцией крыльев вокруг продольной оси туловища птицы и насекомого – это обозначение контурной и частотной образующей сферы или поля вращения. Потому, как и при броске бумеранга, движение крыльев вниз, образуя сферу вращения, проявляет и полевую структуру фазового перехода пространственного тяготения, резонируя с ним. Этим движения крыльев подобно бумерангу не только повторяют структуру фазового пространственного перехода, но и за счёт особой подвижности их связок движутся этой полевой структурой тяготения пространства.

При этом достаточно одного взмаха для начала такого движения крыльев подвижной полевой пространственной структурой. Ведь взмах происходит одновременно двумя крыльями, а потому срединное звено фазового перехода «πи/√2» или доворот может проявляться уже не через 2/3 окружности вращения, а – через 1/3 или через маховый поворот двух крыльев на 120 градусов. Таким образом, первый взмах крыльев птиц и насекомых уже сопровождается «доворотом» «πи/√2», как перпендикулярной к маховому движению циркуляцией крыла. Дело в том, что поскольку крыло в его движении, естественно, не выворачивается на радианную величину «пи» или на 180 градусов, то и взмах вниз переходит не в поворот крыла на 180 градусов, а – в его перекручивание, что структурно и есть образованием пространственного или полевого конуса.

Перекручивание крыла при этом, как подобие скручивания пружины заставляет крылья подниматься вверх без всякого мышечного усилия. Но и подъём крыльев также сопровождается полевым пространственным «доворотом» «πи/√2», также приводящим к перекручиванию (но уже не так явно отражающемуся на рисунке профиля крыла). Этим уже и последующее опускание крыльев происходит от полевой структуры тяготения пространства. Потому и исследователи махового полёта обозначают эти движения (20), вызываемые воздействием пространственной структуры, как принудительные и автоматические. Но и более того, за счёт доворота или перекручивания уже самих крыльев происходит подобие ракетного движения. Ведь контурный доворот или перекручивание крыльев, как контурный конус, проявляет и перпендикулярный к нему конус частотный, от которого и отталкивается восьмеричное движение крыла.



На рисунке выше слева показан вид чайки сзади поднимающей (верх рисунка) и опускающей крылья (низ рисунка). При виде сзади «доворот» «πи/√2» или перекручивание крыла наиболее заметно при опускании крыльев. Исследователи механизма машущего полёта описывают образование видимого пространственного конуса в движении крыльев птиц и насекомых, как (20,21) траекторию крыла, представляющую собой «сложную кривую в виде восьмёрки и нуля, а также их сочетания». Восьмёрка и есть следствием перекручивания крыла, которое, в свою очередь, есть следствием образования пространственного или полевого конуса. А последний образуется за счёт поворота «πи/√2», как происходящего одновременно в двух перпендикулярных плоскостях (круговых слоях), чем он и становится именно «доворотом» примерно на 37 градусов относительно наблюдаемой оси.

При этом в массовом пространстве, как в ощущаемом, взмахи крыльев образуют окружность, а в предмассовом пространстве, как в наблюдаемом, и образуется восьмёрка от пространственного конуса. Этим и объясняется сочетание нуля и восьмёрки в траектории крыла. И можно сказать, что и любой полевой диполь (например, магнитного поля) – это также проявление срединного звена «πи/√2» пространственного фазового перехода.

Т.о., перекручивание крыльев за счёт пространственного «доворота» «πи/√2» определённой частоты вращения начальной силовой сферы (от первичного взмаха крыльев) не только порождает дальнейшей инерционное движение крыла, но и создаёт тяговую силу движения. Или, как пишет исследователь (20), насекомое не только машет крыльями верх и вниз, но – и по горизонтальному кругу, как при гребле на лодке. Получается, что после первичного взмаха крыльев уже сама структура пространства, как структура фазового перехода, возвратно движет крылья, которые при этом ещё и отталкиваются от этой структуры, создавая силу тяги. И птица или насекомое затрачивает энергию лишь на первичный взмах после прерывания полёта или на изменение скорости и направления полёта.

Последующие (после первичного взмаха) движения крыльев, вызываемые фазовым пространственным переходом, не только отталкиваются от частотного перпендикулярного пространственного конуса, но, как и в ракетном движении, – от инерционной силовой цепочки, образуемой цикличными взмахами крыльев. Такая силовая цепочка, обозначаемая исследователем (20) вихревыми кольцами, и изображена на рисунке верху слева. Этим и объясняется огромная скорость полёта, достигаемая птицами.